深入探索 Gnosis Condition Token 和 LSMR 算法

概述

在预测市场发展的早期阶段，Gnosis 编写了 Condition tokens Contract 和 Condition tokens Market Maker。其中 Condition tokens 机制仍被 Polymarket 平台使用，读者可以阅读 How Polymarket Works 了解更多信息。

但是 Polymarket 并没有使用 Condition tokens 的核心特性，即组合预测市场。在预测市场在传统金融发展过程中，Robin Hanson 编写了两篇论文，这两篇论文提出了 LSMR 算法。读者可以在 Implementing Hanson’s Market Maker 内找到 Hanson 论文的链接和对 LSMR 的介绍。另有材料指出 Hanson 的论文实际上是 AMM 算法的思想来源。Gnosis 基于 LSMR 算法实现了 Condition tokens Market Maker 合约，该合约内部实现了 LSMR 算法和常规的恒定积算法(就是 Uniswap v2 使用的 AMM 算法)。

在本文中，我们主要介绍 Gnosis 为预测市场编写的两个智能合约的具体实现以及内部的代码，特别是 Condition token 内基于 ECMH 算法设计的组合预测市场的特性，以及 Maket Maker 合约内的 LSMR 算法。由于恒定积算法已经人尽皆知，所以本文不会介绍 LSMR 算法的这一部分。本文也不会介绍具体的数学函数实现，LSMR 算法只依赖于简单的 exp 和 ln 函数，这些函数的数学实现并不困难，在 Gnosis 编写代码时，这些数学函数还需要自己实现，但目前已经存在了 FixedPointMathLib 等数学库，这些库内对常规数学函数都进行了高效实现。

conditional tokens contracts

市场初始化

在进行预测市场初始化时，我们需要 oracle 和 questionId 参数，其中 oracle 代表预测市场最终清算数据的预言机地址，而 questionId 是一个由创建者指定的代表预测市场 ID 的数据，有可能是一个包含所有内容的 IPFS。在预测市场初始化时，我们还需要一个参数 outcomeSlotCount，该参数代表输出结果的条件数量。比如存在如下预测市场处理以下两个问题:

在 Alice, Bob 和 Carol 内进行选择(choice)
得分是 high 还是 low(score)

我们将其拆分为两部分来看，即 Condition 1 代表选择 Alice / Bob / Carol，而 Condition 2 代表得分是 high / low。用户可以在 Condition 1 和 Condition 2 内任意选项进行选择组合，组合的最终所有结果如下图所示:

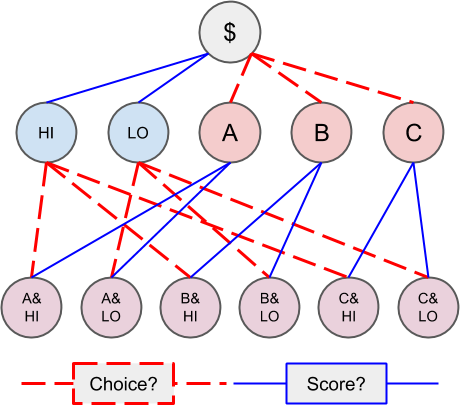
Cond Market slots

比如我们可以先选择 Condition 2 内的 HI 然后选择 Condition 1 内的 Alice(即上图内的 A)，最后我们就获得 A & HI 的结果。当然，此处的选择顺序并不重要。我们可以将 Condition 视为对预测市场结果的约束，施加约束越多意味着结果越准确，最终获胜后获得的资金越多。

在智能合约内，上述 Condition 1 和 Condition 2 初始化可以使用如下代码完成。当然假如预测市场内存在更多 Condition 都可以使用此代码依次进行初始化。此处存在 payoutNumerators 参数，该参数会与 payoutDenominator 参数配合确定最终结算时，每一个 outcomeSlot 可以获得的代币比例。而 outcomeSlot 表示每一个 Condition 输出的结果的数量，比如上文内的 Condition 1 的 outcomeSlot = 3，而 Condition 2 的 outcomeSlot = 2。

此处为什么存在两个数列，这是因为 solidity 内无法存储分数，所以此处选择了对分数的分子和分母部分进行单独存储，但在 prepareCondition 内，我们只会进行初始化操作而不会填入任何数据，具体的数据填入会在后文介绍的 reportPayouts 内完成。

/// @dev This function prepares a condition by initializing a payout vector associated with the condition.
/// @param oracle The account assigned to report the result for the prepared condition.
/// @param questionId An identifier for the question to be answered by the oracle.
/// @param outcomeSlotCount The number of outcome slots which should be used for this condition. Must not exceed 256.
function prepareCondition(address oracle, bytes32 questionId, uint outcomeSlotCount) external {
    // Limit of 256 because we use a partition array that is a number of 256 bits.
    require(outcomeSlotCount <= 256, "too many outcome slots");
    require(outcomeSlotCount > 1, "there should be more than one outcome slot");
    bytes32 conditionId = CTHelpers.getConditionId(oracle, questionId, outcomeSlotCount);
    require(payoutNumerators[conditionId].length == 0, "condition already prepared");
    payoutNumerators[conditionId] = new uint[](outcomeSlotCount);
    emit ConditionPreparation(conditionId, oracle, questionId, outcomeSlotCount);
}

此处我们需要注意 conditionId 的计算方法，具体计算方法如下:

function getConditionId(address oracle, bytes32 questionId, uint outcomeSlotCount) internal pure returns (bytes32) {
    return keccak256(abi.encodePacked(oracle, questionId, outcomeSlotCount));
}

上述介绍的 prepareCondition 函数完成了最初的预测市场初始化，接下来，我们介绍预测市场结束时，预言机如何对预测市场内传入参数以备最后清算:

function reportPayouts(bytes32 questionId, uint[] calldata payouts) external {
    uint outcomeSlotCount = payouts.length;
    require(outcomeSlotCount > 1, "there should be more than one outcome slot");
    // IMPORTANT, the oracle is enforced to be the sender because it's part of the hash.
    bytes32 conditionId = CTHelpers.getConditionId(msg.sender, questionId, outcomeSlotCount);
    require(payoutNumerators[conditionId].length == outcomeSlotCount, "condition not prepared or found");
    require(payoutDenominator[conditionId] == 0, "payout denominator already set");

    uint den = 0;
    for (uint i = 0; i < outcomeSlotCount; i++) {
        uint num = payouts[i];
        den = den.add(num);

        require(payoutNumerators[conditionId][i] == 0, "payout numerator already set");
        payoutNumerators[conditionId][i] = num;
    }
    require(den > 0, "payout is all zeroes");
    payoutDenominator[conditionId] = den;
    emit ConditionResolution(conditionId, msg.sender, questionId, outcomeSlotCount, payoutNumerators[conditionId]);
}

首先，我们通过利用 msg.sender 作为参数计算 conditionId 的行为避免了非 oracle 调用 reportPayouts 函数，换言之，reportPayouts 只能由 oracle 调用。然后，reportPayouts 将 oracle 传入的 payouts 内的内容依次写入 payoutNumerators 内部，Oracle 可以输入 [1, 0, 0] 这种数组，代表输出 0 分别获得 1 的奖励，而其他输出都不会获得奖励。此处的 payoutDenominator 会在函数内部使用 den = den.add(num); 进行计算。

Split Position

接下来，我们主要介绍用户如何参与上述预测市场，需要额外说明的是，我们允许用户进行对自己的投注增加多个 condition 进行联合限制。比如，使用上一个案例，我们允许用户对自己的投注施加 condition 1 内的 50+ bps decrease ，等效于同时投注 50+ bps decrease & Yes 和 50+ bps decrease & No。接下来，用户也可以继续为自己的投注增加限制，比如继续施加 condition 2 内的 Yes 限制，这样用户最终获得了 50+ bps decrease & Yes。

在实际中，这种不断施加限制的行为被称为 split。我们可以把一个包含多种情况的头寸切分为一系列限制更多的头寸，比如用户可以将 50+ bps decrease 拆分为 50+ bps decrease & Yes 和 50+ bps decrease & No。然后按市场价格卖出 50+ bps decrease & No，获取资金。手动拆分可以被视为进行类似数学上因子分解的逻辑，上述拆分可以使用:

50+ bps decrease = 
	(50+ bps decrease & Yes) | (50+ bps decrease & No)

当然，在最初的情况下，用户直接向预测市场内投入 USDC 等资金(在合约内部，我们使用 collateralToken 描述) 换取预测结果，我们可以使用:

$ = Yes | No
$ = 50+ bps decrease | 25 bps decrease | No change | 25+ bps increase

但是，我们不可以进行如下操作:

50+ bps decrease & Yes = 50+ bps decrease | Yes
$ = (50+ bps decrease | 25 bps decrease) | (25 bps decrease | No change)

我们可以看到上述操作的问题是都出现了拆分结果重合的情况。在智能合约内，我们使用 indexSet 描述不同的结果，我们可以规定上述 8 种情况都可以使用一个特定的 bit 表示，比如 0b10000000 代表 50+ bps decrease & Yes，而 0b01000000 代表 50+ bps decrease & No，显然 0b11000000 表示 50+ bps decrease(更准确的说，应该是表示 50+ bps decrease & Yes | 50+ bps decrease & No)。在 Gnosis 文档内，存在以下图片:

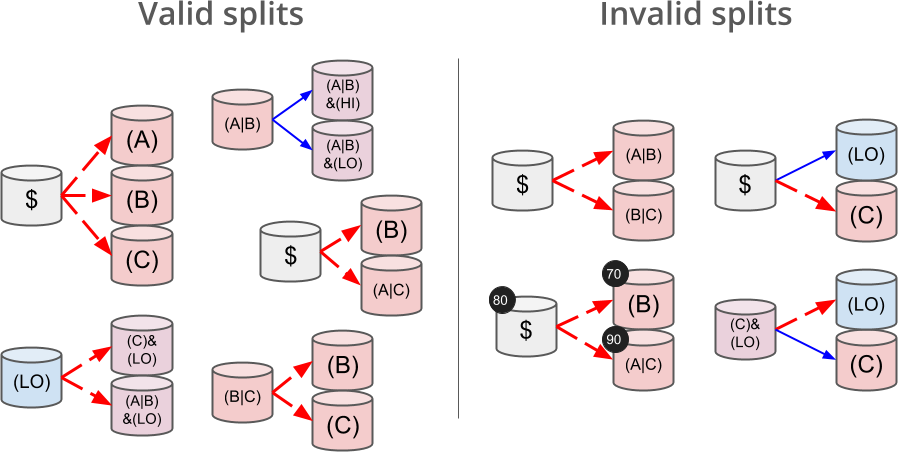
Valid vs Invalid splits

在 splitPosition 代码内，我们的函数定义如下:

function splitPosition(
    IERC20 collateralToken,
    bytes32 parentCollectionId,
    bytes32 conditionId,
    uint[] calldata partition,
    uint amount
) external {

我们额外需要注意此处的 conditionId。正如上文所述，我们会根据预测市场标的的需求创建多个 condition。此处的 conditionId 就是指准备在此次 split 过程中选择哪种 condition 进行切分，比如将 50+ bps decrease 且分为对应的 Yes 和 No ，此处的 conditionId 就是 condition 2(某种利率变化是否会发生) 对应的 id。

上述函数定义内的 uint[] calldata partition 数组内容是用户希望拆分获得的 indexSet。此处的 indexSet 需要与 conditionId 内设置的长度对应。我们使用如下方法确定用户输入的 partition 的每一项长度都符合要求，并且保证拆分后的结果内没有拆分重合的情况发生:

// For a condition with 4 outcomes fullIndexSet's 0b1111; for 5 it's 0b11111...
uint fullIndexSet = (1 << outcomeSlotCount) - 1;
uint freeIndexSet = fullIndexSet;

for (uint i = 0; i < partition.length; i++) {
	  uint indexSet = partition[i];
    require(indexSet > 0 && indexSet < fullIndexSet, "got invalid index set");
    require((indexSet & freeIndexSet) == indexSet, "partition not disjoint");
    freeIndexSet ^= indexSet;
    
    // 省略其他代码
}

我们使用 freeIndexSet 并不断使用 XOR 指令在内部累计之前的 indexSet 的内容，假如 (indexSet & freeIndexSet) != indexSet 就说明 freeIndexSet 之前累积的内容内存在某一个或几个 bit 与当前的 indexSet 重叠，这就会触发失败。

我们需要说明的是，Gnosis 使用了 ERC1155 表示所有的投注代币，这里面临的一个问题是如何确定 ERC1155 的 tokenId。此处我们需要保证在对同一份资产存在不同的拆分方法的情况下，不同的拆分方法获得的最终的代币 tokenId 是一致的，比如下图展示 A & Yes 两种获得方法，但我们需要保证这两种方法可以获得一致的代币。

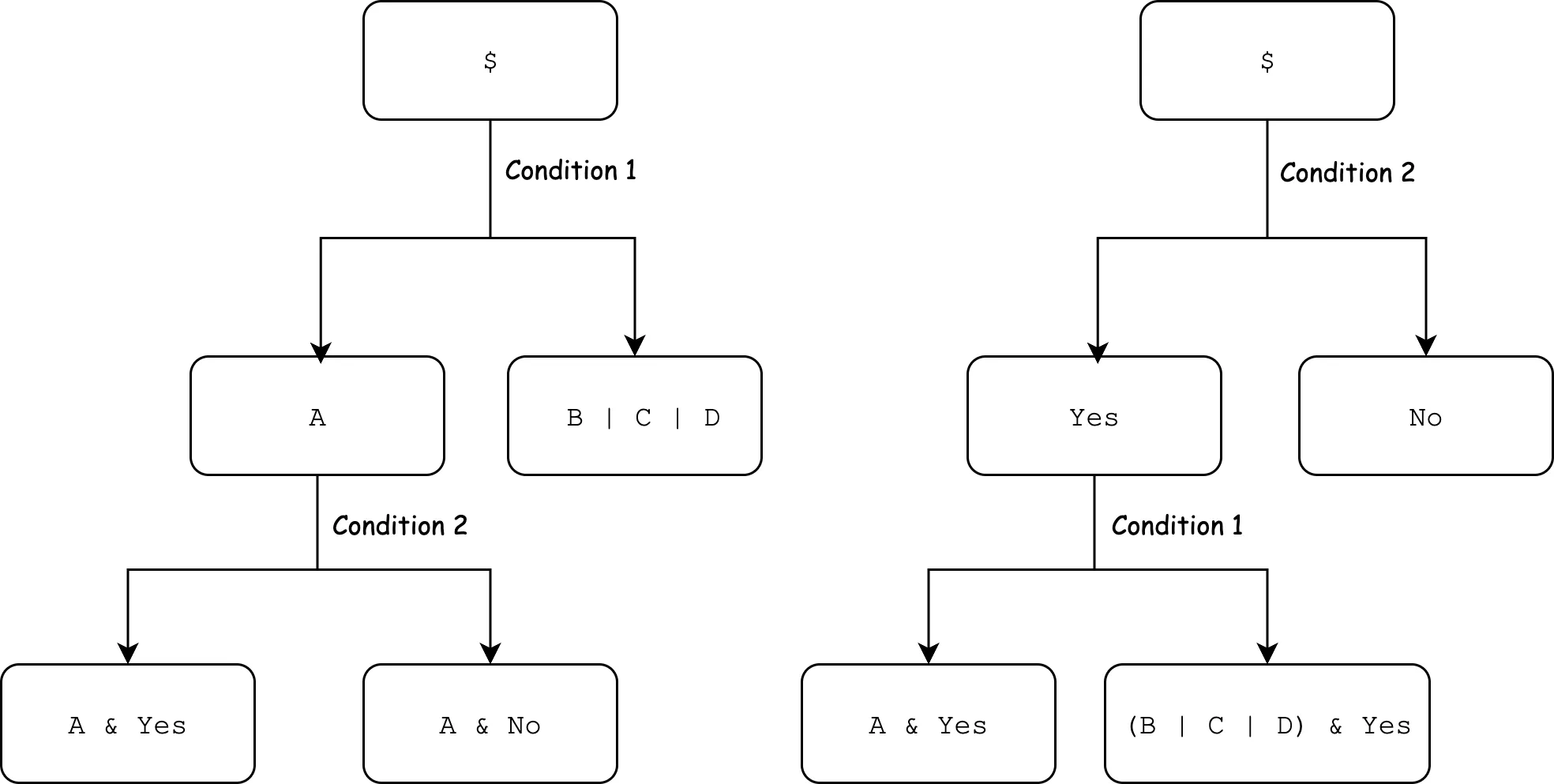
Split With Different Condition

在密码学领域中，存在一种被称为 Multiset Hash 的原语。Multiset 是一种数据结构，该数据结构允许每一个元素多次出现，比如我们允许出现 ${a, a, b}$ 这种类型的集合，其中 $a$ 的 multiplicity 为 1。我们一般使用 $H({a_1, \dots, a_n})$ 描述这种原语。

Multiset Hash 有一种经典的基于 hashing to curve points 和 ecAdd 的构建方法，该方法来自 Elliptic Curve Multiset Hash。在 ECMH 论文内，哈希函数的计算如下: $$ H(M) = \sum_{a \in A}M(a) \cdot \hat{H}(a) $$ 此处的 $\hat{H}$ 指的是一种正常的哈希函数，比如 keccak256 等。而此处的 $M(a)$ 指的是在 Multiset 内的某一个元素出现的此处，比如在 ${a,a,b}$ 内的 $M(a) = 2$。显然，该哈希函数可以实现 $H(M_1 + M_2) = H(M_1) + H(M_2)$，但此处的 $+$ 都发生在椭圆曲线有限域内部。在本文中，我们使用 bn254(也被称为 alt_bn_128)，该椭圆曲线是配对友好曲线，常被用于 zk 应用，其有限域大小大概为 $2^{254}$，但安全性只有 128bit。

对于上图的案例，我们可以使用 Multiset Hash 进行计算，比如左侧的计算如下:

H(Condition 1) + H(Condition 2) = H(Condition 1 + Condition 2)

而右侧的计算如下:

H(Condition 2) + H(Condition 1) = H(Condition 2 + Condition 1)

由于加法存在交换律，所以上述两种计算结果是相同的。但在实际代码中，我们不仅需要给定 Condition 还需要给定一个输出结果，因为对于上图内的 Condition 1，其最多支持 4 个输出，我们需要使用 indexSet 给定当前节点的输出。此处的 indexSet 是一种二进制表示某种结果是否存在的 bitmap。比如:

A = 0b1000
B = 0b0100
C = 0b0010
D = 0b0001

A | B = 0b1100
A | B | C = 0b1110

在 CTHelpers 内存在 getCollectionId 函数，该函数用于给定 parentCollectionId 以及 conditionId 和 indexSet 输出目标预测市场选项对应的 collectionId。给定的 parentCollectionId 内部其实包含一个 Multiset，其内容是过去所有在 split 过程中使用的 Condition 及其 indexSet。所以 collectionId 对应是的某一个预测市场选项背后对应所有的 Condition。在计算 tokenId 时，我们会使用 getPositionId 函数，该函数将 collectionId 与 collateralToken 拼接起来计算具体的 tokenId。

function getPositionId(IERC20 collateralToken, bytes32 collectionId) internal pure returns (uint) {
    return uint(keccak256(abi.encodePacked(collateralToken, collectionId)));
}

我们先不考虑 getCollectionId 的实现细节，而是直接利用该函数继续完成 splitPosition:

for (uint i = 0; i < partition.length; i++) {
    uint indexSet = partition[i];
    require(indexSet > 0 && indexSet < fullIndexSet, "got invalid index set");
    require((indexSet & freeIndexSet) == indexSet, "partition not disjoint");
    freeIndexSet ^= indexSet;
    positionIds[i] = CTHelpers.getPositionId(collateralToken, CTHelpers.getCollectionId(parentCollectionId, conditionId, indexSet));
    amounts[i] = amount;
}

此处的 CTHelpers.getPositionId 使用用户输入 parentCollectionId 和 conditionId 以及 indexSet 来计算 CollectionId。获得 ColletcionId 后，我们继续计算 positionId。为了进一步分析不同的 split 方式，我们需要介绍在市场内不同选项 split 类型:

将一个完整的选项进行拆分，比如使用 Condition 将 collateral 进行拆分，或者使用一个之前没有使用某种 Condition 的代币使用该 Condition 拆分
将一个部分选项进行拆分，比如将 A | B 拆分为 A 和 B

在以下代码中，freeIndexSet == 0 代表完整选项的拆分，此处要考虑的额外情况是假如用户输入的是 parentCollectionId 是 0 代表用户希望将 collateral 拆分，此时我们将用户的 collateralToken 转入当前智能合约以备最后清算。而假如用户输入的 parentCollectionId != 0 则说明用户希望将 parentCollection 使用一种新的 Condition 进行拆分，此时我们会调用 burn 函数销毁 ERC1155 代币。

if (freeIndexSet == 0) {
    // Partitioning the full set of outcomes for the condition in this branch
    if (parentCollectionId == bytes32(0)) {
        require(collateralToken.transferFrom(msg.sender, address(this), amount), "could not receive collateral tokens");
    } else {
        _burn(
            msg.sender,
            CTHelpers.getPositionId(collateralToken, parentCollectionId),
            amount
        );
    }
} else {
    // Partitioning a subset of outcomes for the condition in this branch.
    // For example, for a condition with three outcomes A, B, and C, this branch
    // allows the splitting of a position $:(A|C) to positions $:(A) and $:(C).
    _burn(
        msg.sender,
        CTHelpers.getPositionId(collateralToken,
            CTHelpers.getCollectionId(parentCollectionId, conditionId, fullIndexSet ^ freeIndexSet)),
        amount
    );
}

对于部分选项进行的拆分为位于上文代码内的 else 部分中，我们会使用 fullIndexSet ^ freeIndexSet 获得用户输入的 indexSet 的组合，这说明用户希望将形似 A | B 的选项拆分为 A 和 B。这也是为什么我们在 splitPosition 函数内不需要给出要拆分的 position 的 indexSet，我们只需要给出 partition，函数内会使用 partition 拼接出待拆分的 parent node 的 indexSet:

function splitPosition(
    IERC20 collateralToken,
    bytes32 parentCollectionId,
    bytes32 conditionId,
    uint[] calldata partition,
    uint amount
)

在 splitPosition 函数的最后，我们会完成最无聊的一步，即为用户铸造 ERC1155 代币:

_batchMint(
    msg.sender,
    // position ID is the ERC 1155 token ID
    positionIds,
    amounts,
    ""
);
emit PositionSplit(msg.sender, collateralToken, parentCollectionId, conditionId, partition, amount);

Merge Position

与上文介绍的 splitPosition 不同，Merge Position 是 split 的逆向操作，我们可以将多个选项合并为一个头寸。

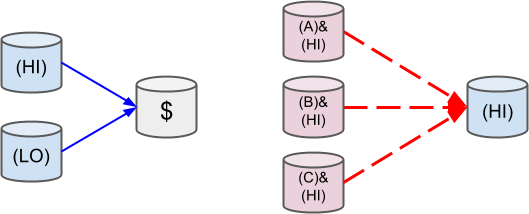
Merge Position

由于 mergePositions 与 splitPosition 是互逆的关系，所以 mergePositions 的定义与 splitPosition 的定义几乎一致:

function mergePositions(
    IERC20 collateralToken,
    bytes32 parentCollectionId,
    bytes32 conditionId,
    uint[] calldata partition,
    uint amount
) external {

用户需要输入待合并的 indexSet 列表，该列表上述定义中的 partition 参数。而 parentCollectionId 是合并目标的 collectionId。对于 mergePositions 的第一部分，代码基本与 splitPositions 是一致的，都是检查用户的输入的 partition 内部不包含交叉情况。另外，我们会将 partition 内的 indexSet 与 conditionId 和 parentCollectionId 结合在一起计算出 positionIds 以备后期 burn 使用。

uint fullIndexSet = (1 << outcomeSlotCount) - 1;
uint freeIndexSet = fullIndexSet;
uint[] memory positionIds = new uint[](partition.length);
uint[] memory amounts = new uint[](partition.length);
for (uint i = 0; i < partition.length; i++) {
    uint indexSet = partition[i];
    require(indexSet > 0 && indexSet < fullIndexSet, "got invalid index set");
    require((indexSet & freeIndexSet) == indexSet, "partition not disjoint");
    freeIndexSet ^= indexSet;
    positionIds[i] = CTHelpers.getPositionId(collateralToken, CTHelpers.getCollectionId(parentCollectionId, conditionId, indexSet));
    amounts[i] = amount;
}

_batchBurn(
    msg.sender,
    positionIds,
    amounts
);

之后，我们会执行真正的 merge 操作，对于那些 merge 后产生某一个 Condition 全部结果的情况，我们会根据 parentCollectionId 的情况决定是直接向用户转出一定数量的 collateralToken 或者为用户直接铸造 parentCollectionId 对应的 token。对于没有产生某一个 Condition 全部结果的情况，我们会使用 fullIndexSet ^ freeIndexSet 计算出用户 merge 后 position 的 indexSet，然后进一步铸造代币。

if (freeIndexSet == 0) {
    if (parentCollectionId == bytes32(0)) {
        require(collateralToken.transfer(msg.sender, amount), "could not send collateral tokens");
    } else {
        _mint(
            msg.sender,
            CTHelpers.getPositionId(collateralToken, parentCollectionId),
            amount,
            ""
        );
    }
} else {
    _mint(
        msg.sender,
        CTHelpers.getPositionId(collateralToken,
            CTHelpers.getCollectionId(parentCollectionId, conditionId, fullIndexSet ^ freeIndexSet)),
        amount,
        ""
    );
}

emit PositionsMerge(msg.sender, collateralToken, parentCollectionId, conditionId, partition, amount);

Redeem Position

所谓的 Redeem position 行为就是在 oracle 报告后，用户将自己手里的代表投注的 ERC1155 进行一种特殊的 Merge 方法，这种 Merge 方法最终可以将投注转化为 collateral token。下图显示了 Redeem 行为:

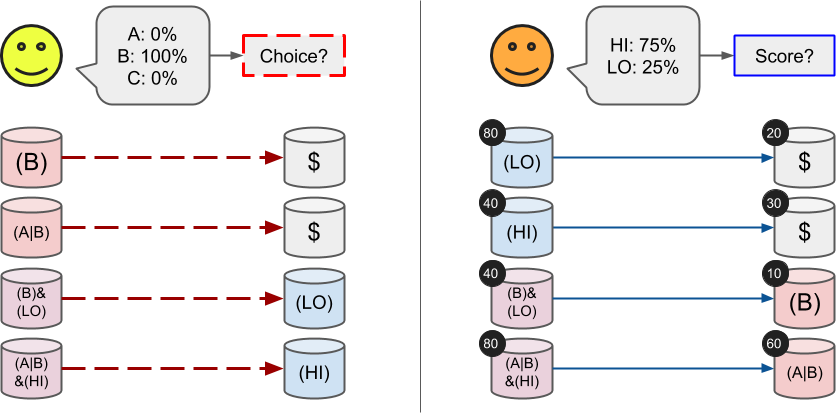
Redeem Position

首先，我们在 redeemPositions 函数中，由于我们可以直接计算出用户持有的 ERC1155 tokenId，此时，我们可以直接调用 balanceOf 获得用户持有的代币数量，所以在最初的函数定义中，我们不需要用户给定 amount 参数:

function redeemPositions(IERC20 collateralToken, bytes32 parentCollectionId, bytes32 conditionId, uint[] calldata indexSets) external {}

此处的所有的参数含义都与 splitPosition 相同，由于 redeem 只会发生在 oracle 报告结果后，所以此处我们需要检查 oracle 是否已经报告了结果:

uint den = payoutDenominator[conditionId];
require(den > 0, "result for condition not received yet");
uint outcomeSlotCount = payoutNumerators[conditionId].length;
require(outcomeSlotCount > 0, "condition not prepared yet");

之后，我们会根据用户输入的 indexSets 和其他信息计算 positionId，然后根据 indexSet 内的内容与 payoutNumerators 内的内容为用户计算可以获得 totalPayout 的数量。最后，我们将 payoutStake 数量的代币 burn 完成操作。

uint totalPayout = 0;

uint fullIndexSet = (1 << outcomeSlotCount) - 1;
for (uint i = 0; i < indexSets.length; i++) {
    uint indexSet = indexSets[i];
    require(indexSet > 0 && indexSet < fullIndexSet, "got invalid index set");
    uint positionId = CTHelpers.getPositionId(collateralToken,
        CTHelpers.getCollectionId(parentCollectionId, conditionId, indexSet));

    uint payoutNumerator = 0;
    for (uint j = 0; j < outcomeSlotCount; j++) {
        if (indexSet & (1 << j) != 0) {
            payoutNumerator = payoutNumerator.add(payoutNumerators[conditionId][j]);
        }
    }

    uint payoutStake = balanceOf(msg.sender, positionId);
    if (payoutStake > 0) {
        totalPayout = totalPayout.add(payoutStake.mul(payoutNumerator).div(den));
        _burn(msg.sender, positionId, payoutStake);
    }
}

在之前的 split 过程中，我们并没有对用户的 split 进行任何限制，用户实际上可以进行如下操作，即对于 A 在进行一次 Condition 1 的 split 使其被切分为 A & A 和 A & (A | B):

A -> [A & A, A & (A | B)]

但在此处的 redeemPositions 中，我们会发现上述行为从经济学上是无用的，进行这种行为只会降低总体收益而不会获得额外的好处。从概率角度分析，该行为会降低自己获胜的概率。

最后，我们需要进行清算操作，该操作也非常简单:

if (totalPayout > 0) {
    if (parentCollectionId == bytes32(0)) {
        require(collateralToken.transfer(msg.sender, totalPayout), "could not transfer payout to message sender");
    } else {
        _mint(msg.sender, CTHelpers.getPositionId(collateralToken, parentCollectionId), totalPayout, "");
    }
}
emit PayoutRedemption(msg.sender, collateralToken, parentCollectionId, conditionId, indexSets, totalPayout);

ECMH 算法实现

在本节中，我们将上一节中介绍的 mutliset hash 算法进行 solidity 实现。ECMH 的原理是将数据的哈希值映射到曲线上(这种行为一般被称为 hashToCurve)，然后将哈希值与之前的数据在椭圆曲线上进行相加。在 Gnosis 代码编写时，BN254 曲线是唯一选择，但是 Pectra 升级后，以太坊主网引入了 BLS12-381 曲线，该曲线也可以进行 ECMH 算法。BN254 曲线最著名的分析是 BN254 For The Rest Of Us。在本文中，我们会介绍其中部分内容，假如读者希望完整了解 BN254 建议阅读原文。

BN254 曲线都存在如下形式: $$ Y^2 = X^3 + b $$ 其中参数 b = 3。另一个重要参数是椭圆曲线域 $\mathbb{F}_p$ 的大小，此类型曲线的大小如下: $$ p = 36x^4 + 36x^3 + 24x^2 + 6x + 1 $$ 其中 BN254 选择的 x = 4965661367192848881。计算结果就是代码内的:

uint constant P = 21888242871839275222246405745257275088696311157297823662689037894645226208583;

有了以上知识，我们就可以分析 getCollectionId 函数的实现。我们第一步需要进行 hashToCurve 操作。简单来说，该操作就是将哈希值视为 x 以此计算对应的 y 点获得曲线上的 $(x, y)$ 坐标。该部分对应如下代码:

uint x1 = uint(keccak256(abi.encodePacked(conditionId, indexSet)));
bool odd = x1 >> 255 != 0;
uint y1;
uint yy;
do {
    x1 = addmod(x1, 1, P);
    yy = addmod(mulmod(x1, mulmod(x1, x1, P), P), B, P); // x^3 + b
    y1 = sqrt(yy);
} while(mulmod(y1, y1, P) != yy);
if(odd && y1 % 2 == 0 || !odd && y1 % 2 == 1)
    y1 = P - y1;

这里需要注意的是，我们将 x1 的第 1 bit 视为当前 x 对应的 y 数值的正负情况。BN254 没有·过多标准化的内容，所以这意味着签名的具体格式等都可以按照开发者的自身需求确定，比如此处的将 x1 的第 1bit 视为 y 正负情况就是开发者自己约定的。

此处的需要注意 keccak256 并不一定是曲线上的点，而且极有可能大于 P。此处我们会使用迭代求解方法不断对 x1 进行迭代直到获得曲线上的点，上文代码内的 do-while 循环就是进行了此操作，mulmod(y1, y1, P) != yy 就是用来判断 y1 是否位于曲线上。最后，我们会使用 odd 和 y1 % 2 取 and 的结果作为是否对 y1 进行调整。

在进行完成上述哈希值向椭圆曲线上点的映射后，我们下一步需要将 parentCollectionId 与上文计算出的 $(x_1, y_1)$ 相加，其中核心的加法(ecAdd)会调用 EVM 内的预汇编合约实现。在此过程中，我们第一步是将 parentCollectionId 转化为曲线上的点 $(x_2, y_2)$。此处需要注意的由于 BN254 内最大的点数值等于 254bit，所以 Gnosis 开发者将前 2 bit 作为 odd ，用来标记 $y_2$ 的正负情况。此处需要额外注意 x2 == 0 的情况，这种情况下，我们并不需要进行 ecAdd 操作，因为此时 parentCollectionId 就是根节点。

uint x2 = uint(parentCollectionId);
if(x2 != 0) {
    odd = x2 >> 254 != 0;
    x2 = (x2 << 2) >> 2;
    yy = addmod(mulmod(x2, mulmod(x2, x2, P), P), B, P);
    uint y2 = sqrt(yy);
    if(odd && y2 % 2 == 0 || !odd && y2 % 2 == 1)
        y2 = P - y2;
    require(mulmod(y2, y2, P) == yy, "invalid parent collection ID");

然后，我们计算出 $(x_2, y_2)$ 数值后，我们可以使用如下代码执行最后的 ecAdd 操作:

(bool success, bytes memory ret) = address(6).staticcall(abi.encode(x1, y1, x2, y2));
require(success, "ecadd failed");
(x1, y1) = abi.decode(ret, (uint, uint));

最后，我们需要使函数输出的 x1 满足之前的前 2 bit 作为 odd 数值的要求，我们会执行如下操作:

if(y1 % 2 == 1)
    x1 ^= 1 << 254;

return bytes32(x1);

以下代码显示了对 0x52ff54f0f5616e34a2d4f56fb68ab4cc636bf0d92111de74d1ec99040a8da118 的 map to curve 的流程，此处我们没有展示哈希的过程，读者可以自行调用一些哈希函数计算结果。以下代码只依赖了 noble-curves 代码库。

import { bn254 } from "@noble/curves/bn254";

const Fp = bn254.fields.Fp;

let x1Field: bigint;
let y1Field: bigint;
let yy: bigint;

const x1 = BigInt(
  "0x52ff54f0f5616e34a2d4f56fb68ab4cc636bf0d92111de74d1ec99040a8da118",
);

const odd = Boolean(x1 >> 255n);

x1Field = Fp.create(x1 + 1n);

while (true) {
  yy = bn254.G1.weierstrassEquation(x1Field);
  try {
    y1Field = Fp.sqrt(yy);
    break;
  } catch {
    x1Field = Fp.create(x1Field + 1n);
  }
}

if ((odd && y1Field % 2n == 0n) || (!odd && y1Field % 2n == 1n)) {
  y1Field = Fp.neg(y1Field);
}

console.log(`x1: ${x1Field}`);
console.log(`y1: ${y1Field}`);

在上述代码内，我们使用 Fp 对象内封装的一系列计算避免了显式的 mod 操作，同时在 noble-curves 实现内，sqrt 函数会自动检查计算出的结果是否符合有限域的要求，所以此处我们没有使用 while 进行判断，而是直接依赖了 sqrt 内部的检测机制。

Condition tokens Market makers

在上一节中，我们主要介绍了 Condition tokens 的内容，我们完成了预测市场内的代币构造。在本节中，我们主要介绍 Gnosis 如何设计算法为这些代币提供流动性。为了完成提供流动性的目的，Gnosis 提供了两种算法:

LSMR 算法，该算法是本节的核心内容
恒定积算法，其实就是 Uniswap v2 使用的算法，本节不会介绍

本节的代码可以在 Conditional Tokens Automated Market Makers (AMM) 仓库内找到。此仓库内导入了 @gnosis.pm/util-contracts，该合约提供了数学计算的一些功能。

Factory 部署

我们首先介绍如何部署一个 LSMR 算法市场，具体代码如下:

function createLMSRMarketMaker(ConditionalTokens pmSystem, IERC20 collateralToken, bytes32[] calldata conditionIds, uint64 fee, Whitelist whitelist, uint funding)
    external
    returns (LMSRMarketMaker lmsrMarketMaker)
{
    lmsrMarketMaker = LMSRMarketMaker(createClone(address(implementationMaster), abi.encode(pmSystem, collateralToken, conditionIds, fee, whitelist)));
    collateralToken.transferFrom(msg.sender, address(this), funding);
    collateralToken.approve(address(lmsrMarketMaker), funding);
    lmsrMarketMaker.changeFunding(int(funding));
    lmsrMarketMaker.resume();
    lmsrMarketMaker.transferOwnership(msg.sender);
    emit LMSRMarketMakerCreation(msg.sender, lmsrMarketMaker, pmSystem, collateralToken, conditionIds, fee, funding);
}

该函数的参数中较为特殊的是:

pmSystem 就是上文介绍的 ConditionalTokens
whitelist 用于限制交易函数的调用者，当我们将 whitelist 设置为零地址后，相当于 AMM 中的交易函数可以被任何人调用
funding 用于为 AMM 合约提供最初的代币，此处输入的 funding 会被用于在 ConditionalTokens 合约内 split 为所有类型的 conditions token

我们首先使用 createClone 方法使用较低的字节码成本部署一个 implementationMaster 的代理合约，底层原理其实是 EIP-1167。我们先跳过部署问题，先继续分析其他代码，我们会在本小节最后介绍 clone 的运行原理。但此处，我们直接部署后的 LSMR 市场处于 Paused 状态。

后续代码中的 lmsrMarketMaker.changeFunding(int(funding)); 完成了我们在上文介绍函数参数时的将 funding 用于初始化的过程。此处，我们可以简单看一下 changeFunding 的实现:

function changeFunding(int fundingChange)
    public
    onlyOwner
    atStage(Stage.Paused)
{
    require(fundingChange != 0, "funding change must be non-zero");
    // Either add or subtract funding based off whether the fundingChange parameter is negative or positive
    if (fundingChange > 0) {
        require(collateralToken.transferFrom(msg.sender, address(this), uint(fundingChange)) && collateralToken.approve(address(pmSystem), uint(fundingChange)));
        splitPositionThroughAllConditions(uint(fundingChange));
        funding = funding.add(uint(fundingChange));
        emit AMMFundingChanged(fundingChange);
    }
    if (fundingChange < 0) {
        mergePositionsThroughAllConditions(uint(-fundingChange));
        funding = funding.sub(uint(-fundingChange));
        require(collateralToken.transfer(owner(), uint(-fundingChange)));
        emit AMMFundingChanged(fundingChange);
    }
}

实际上，该函数十分简单，当用户输入的 fundingChange > 0 时就会将输入资产 split 为所有类型的 condition token，反之则会 merge 所有类型的 condition tokens 并将资产转移给 owner。注意，该函数只能在市场处于 Paused 情况下才可以运行。

lmsrMarketMaker.resume(); 用于修改市场状态，将市场状态修改为 Running：

function pause() public onlyOwner atStage(Stage.Running) {
    stage = Stage.Paused;
    emit AMMPaused();
}

function resume() public onlyOwner atStage(Stage.Paused) {
    stage = Stage.Running;
    emit AMMResumed();
}

最后，我们将 owner 控制权转移给部署者，在此前，合约的 owner 其实是 factory 合约自身，在此处才真正将控制权转移给了用户。

然后，我们介绍 clone 方法。由于我们需要向 LMSRMarketMaker 内进行变量的初始化，所以我们需要包含初始化参数的 clone 方法。一种常规的方法是使用 clones-with-immutable-args 方法，该方法会将用户输入的参数附带到 create 产生的字节码最后，但是该方法并不适用于目前的 Gnosis 的合约，因为 Gnosis 合约会进行大量的存储操作和计算，所以我们需要一种方法可以几乎完整实现 solidity 构造器的所有功能，为了实现此目的，Gnosis 在合约 create 初始化时的 init code 内增加了很多有趣的功能。

在此处，我们先简单介绍一下该方法的原理。众所周知，智能合约在部署时，以太坊客户端会首先执行 init code 获得字节码，在 init code 内部，我们会进行存储槽初始化和 immutable 参数拼接等功能。假如读者对此不熟悉，可以阅读我在 4seas 课程给出的教学材料自底向上学习以太坊（三）：智能合约开发中的构造器、函数定义与存储布局

为了实现部署过程中，部署出的最小化代理合约的存储槽是被初始化的，Gnosis 修改了最小化代码的字节码，最重要的修改时增加了对部署者的 cloneConstructor(bytes) 函数的 DELEGATE CALL 调用以此实现合约存储初始化。

我们此处展示一下 create2Clone 方法的实现:

function create2Clone(address target, uint saltNonce, bytes memory consData) internal returns (address result) {
    bytes memory consPayload = abi.encodeWithSignature("cloneConstructor(bytes)", consData);
    bytes memory clone = new bytes(consPayload.length + 99);

    assembly {
        mstore(add(clone, 0x20),
            0x3d3d606380380380913d393d73bebebebebebebebebebebebebebebebebebebe)
        mstore(add(clone, 0x2d),
            mul(address, 0x01000000000000000000000000))
        mstore(add(clone, 0x41),
            0x5af4602a57600080fd5b602d8060366000396000f3363d3d373d3d3d363d73be)
        mstore(add(clone, 0x60),
            mul(target, 0x01000000000000000000000000))
        mstore(add(clone, 116),
            0x5af43d82803e903d91602b57fd5bf30000000000000000000000000000000000)
    }

    for(uint i = 0; i < consPayload.length; i++) {
        clone[99 + i] = consPayload[i];
    }

    bytes32 salt = keccak256(abi.encode(msg.sender, saltNonce));

    assembly {
        let len := mload(clone)
        let data := add(clone, 0x20)
        result := create2(0, data, len, salt)
    }
    
    require(result != address(0), "create2 failed");
}

此处的 consPayload 就是在准备调用部署者 cloneConstructor 函数的 calldata，然后我们在最后使用 for 循环将生成的 calldata 拼接到了部署字节码的最后。

我们可以简单看一下此处给出的字节码进行了哪些操作。第一段字节码如下:

3d3d606380380380913d393d73 [bebebebebebebebebebebebebebebebebebebe]

可以翻译为:

RETURNDATASIZE // 此处的 RETURNDATASIZE 可以直接视为 PUSH0，该代码编写时，PUSH0 还不存在
RETURNDATASIZE
PUSH1 63 // 此处的 63 是指不包含调用 delegate call 调用的 init code 的长度
DUP1
CODESIZE // 读取 init code 字节码的长度
SUB // 执行减法操作后，我们就可以获得刚刚 for 循环拼接到 init code 后的 delegate calldata 长度
DUP1
SWAP2
RETURNDATASIZE
CODECOPY // 将拼接的 calldata 读取到内存中
RETURNDATASIZE
PUSH20 bebebebebebebebebebebebebebebebebebebe

上述的 bebebebebebebebebebebebebebebebebebebe 实际上是一个占位地址，我们立即使用 msg.sender 进行了替换，具体使用了以下代码:

mstore(add(clone, 0x2d),
    mul(address, 0x01000000000000000000000000))

后续 5af4602a57600080fd5b 字节码完成了最终的 Delegate call 调用，并根据返回值确定 delegate call 是否成功，假如没有成功，那么会直接触发 revert 终止部署。然后，后续所有的字节码都是 EIP1167 内给出的，当然，读者也可以 solady 的 LibClone.sol 内看到该字节码的分析，也有另一种选择是阅读笔者之前编写的 EVM底层探索:字节码级分析最小化代理标准EIP1167。

一般来说，更加现代的方法是在部署合约内实现 init 函数，factory 直接 clone 部署合约，然后工厂合约部署完成合约后，直接调用 init 方法初始化。但是此处 Gnosis 不使用该方法是存在原因的，因为 LSMR 市场合约的初始化较为复杂，使用 init 方法在 gas 成本上没有任何优势。

初始化

在上文，我们介绍了部署过程中，部署出的代理合约会调用部署者的 cloneConstructor 函数实现初始化，在本节中，我们将着重分析 cloneConstructor 函数。该函数使用以下代码对存储进行了初始化:

_owner = msg.sender;

// Validate inputs
require(address(_pmSystem) != address(0) && _fee < FEE_RANGE);
pmSystem = _pmSystem;
collateralToken = _collateralToken;
conditionIds = _conditionIds;
fee = _fee;
whitelist = _whitelist;

为了保证存储初始化时所有的 slot 都是正确的，我们可以观察到存在 LMSRMarketMakerData 合约，该合约既被 LMSRMarketMakerFactory 继承也被 LMSRMarketMaker 继承。此处可能有读者会发现，LMSRMarketMaker 继承的其实是 MarketMaker 合约，但是 MarketMaker 合约的存储结构与 LMSRMarketMakerData 是一致的。

接下来，我们计算当前系统总共存在多少种 Condition token 的输出可能。显然，我们可以通过 $\prod_{i=0}^n \text{outCome}_i$ 计算获得。以下代码除了使用 $\prod_{i=0}^n \text{outCome}_i$ 计算 atomicOutcomeSlotCount 数值外，还在 outcomeSlotCounts 内部缓存了 getOutcomeSlotCount 的输出，避免后续调用 getOutcomeSlotCount 函数增加 gas 成本。

atomicOutcomeSlotCount = 1;
outcomeSlotCounts = new uint[](conditionIds.length);
for (uint i = 0; i < conditionIds.length; i++) {
    uint outcomeSlotCount = pmSystem.getOutcomeSlotCount(conditionIds[i]);
    atomicOutcomeSlotCount *= outcomeSlotCount;
    outcomeSlotCounts[i] = outcomeSlotCount;
}
require(atomicOutcomeSlotCount > 1, "conditions must be valid");

最后，我们会计算出当前系统内所有正常的 Condition token 的 collection id(与上文中的 PositionId 概念是一致的)并将其记录在存储槽内部:

collectionIds = new bytes32[][](conditionIds.length);
_recordCollectionIDsForAllConditions(conditionIds.length, bytes32(0));

stage = Stage.Paused;
emit AMMCreated(funding);

此处我们主要关注 _recordCollectionIDsForAllConditions 方法。在上文，我们介绍过 Condition 构成的不同组合类似有向无环图(DAG)。所以 _recordCollectionIDsForAllConditions 核心目的是遍历该 DAG 并获得所有节点的 Position id。此处使用了递归算法，该算法并不复杂，读者可以自行阅读。

function _recordCollectionIDsForAllConditions(uint conditionsLeft, bytes32 parentCollectionId) private {
    if(conditionsLeft == 0) {
        positionIds.push(CTHelpers.getPositionId(collateralToken, parentCollectionId));
        return;
    }

    conditionsLeft--;

    uint outcomeSlotCount = outcomeSlotCounts[conditionsLeft];

    collectionIds[conditionsLeft].push(parentCollectionId);
    for(uint i = 0; i < outcomeSlotCount; i++) {
        _recordCollectionIDsForAllConditions(
            conditionsLeft,
            CTHelpers.getCollectionId(
                parentCollectionId,
                conditionIds[conditionsLeft],
                1 << i
            )
        );
    }
}

在上述过程中，在 Condition token 内讨论的对一个选项进行多次同一个 Condition split 的可能性彻底消失了，因为上述方法只会产生严格的只使用一个 Condition 的代币。

LSMR 算法

在介绍具体的 LSMR 算法前，我们需要首先阅读 MarketMaker.sol 文件内的 trade 函数，该函数用于给定代币输出数量列表进行交易，该函数的定义如下:

function trade(int[] memory outcomeTokenAmounts, int collateralLimit)
    public
    atStage(Stage.Running)
    onlyWhitelisted
    returns (int netCost)
{

此处的 outcomeTokenAmounts 是用户输入的所希望获得的代币输出，特别需要注意，该列表的长度等于上文初始化时计算出的 atomicOutcomeSlotCount。比如假如当前市场内存在第一个 Condition 内部包含 A, B, C，第二个 Condition 内部包含 X, Y，第三个 Condition 内部包含 I, J, K。那么，列表内的每一个项分别代表:

/// A&X&I == 0
/// B&X&I == 1
/// C&X&I == 2
/// A&Y&I == 3
/// B&Y&I == 4
/// C&Y&I == 5
/// A&X&J == 6
/// B&X&J == 7
/// C&X&J == 8
/// A&Y&J == 9
/// B&Y&J == 10
/// C&Y&J == 11
/// A&X&K == 12
/// B&X&K == 13
/// C&X&K == 14
/// A&Y&K == 15
/// B&Y&K == 16
/// C&Y&K == 17

当然，我们也可以直接使用 generateAtomicPositionId 获得每一个 index 对应的 Position Id。另外，我们看到 outcomeTokenAmounts 是一个 int 类型的列表，这是因为用户可以通过正负表示自己希望获得某种代币还是给出某种代币。假如是负数，代表用户希望将代币卖回给市场，但假如为正数则代表用户希望从市场内买入某种代币。

进入 trade 函数后，我们第一步需要校验用户输入的 outcomeTokenAmounts 的长度与 atomicOutcomeSlotCount 是否一致，并调用 calcNetCost 计算出当前 LSMR 算法要求的 collateral token 的输入数量。之后，直接调用 calcMarketFee 计算出交易所需要的手续费。此处的 calcMarketFee 实现为 outcomeTokenCost * fee / FEE_RANGE;。最后，检查计算出的结果是否满足用户给定的 collateralLimit，这与传统 AMM 内的滑点检查是一致的。

require(outcomeTokenAmounts.length == atomicOutcomeSlotCount);

// Calculate net cost for executing trade
int outcomeTokenNetCost = calcNetCost(outcomeTokenAmounts);
int fees;
if(outcomeTokenNetCost < 0)
    fees = int(calcMarketFee(uint(-outcomeTokenNetCost)));
else
    fees = int(calcMarketFee(uint(outcomeTokenNetCost)));

require(fees >= 0);
netCost = outcomeTokenNetCost.add(fees);

require(
    (collateralLimit != 0 && netCost <= collateralLimit) ||
    collateralLimit == 0
);

这里需要注意的是 outcomeTokenNetCost 也是存在正负的，其中正数代表用户需要支付给 LSMR Market 的资金数量而负数代表用户从 LSMR Market 内获得的资金数量。所以此处的 netCost = outcomeTokenNetCost.add(fees); 无论正负都可以为用户施加手续费，即对于获得资金的负数情况，由于增加了 fees 导致用户获得资金减少；而对于支付资金的正数情况，由于增加了 fees 用户需要额外支付手续费进入 LSMR Market。

对 outcomeTokenNetCost > 0 即用户需要向 Market 发送资产的情况，我们会讲用户的资产转移到合约内部，然后调用 Condition token 合约的 split 函数将用户资产 split 为 Condition 代币:

if(outcomeTokenNetCost > 0) {
    require(
        collateralToken.transferFrom(msg.sender, address(this), uint(netCost)) &&
        collateralToken.approve(address(pmSystem), uint(outcomeTokenNetCost))
    );

    splitPositionThroughAllConditions(uint(outcomeTokenNetCost));
}

splitPositionThroughAllConditions 使用了如下双层 for 循环遍历之前存储的 collectionIds 和 conditionIds 实现 split 行为:

function splitPositionThroughAllConditions(uint amount)
    private
{
    for(uint i = conditionIds.length - 1; int(i) >= 0; i--) {
        uint[] memory partition = generateBasicPartition(outcomeSlotCounts[i]);
        for(uint j = 0; j < collectionIds[i].length; j++) {
            pmSystem.splitPosition(collateralToken, collectionIds[i][j], conditionIds[i], partition, amount);
        }
    }
}

对于 mergePositionsThroughAllConditions 函数，该函数内部也存在类似结构，只是将 splitPosition 替换为 mergePositions 而已。然后，我们处理可能存在的 ERC1155 代币转入的情况，对应的代码如下:

bool touched = false;
uint[] memory transferAmounts = new uint[](atomicOutcomeSlotCount);
for (uint i = 0; i < atomicOutcomeSlotCount; i++) {
    if(outcomeTokenAmounts[i] < 0) {
        touched = true;
        // This is safe since
        // 0x8000000000000000000000000000000000000000000000000000000000000000 ==
        // uint(-int(-0x8000000000000000000000000000000000000000000000000000000000000000))
        transferAmounts[i] = uint(-outcomeTokenAmounts[i]);
    }
}
if(touched) pmSystem.safeBatchTransferFrom(msg.sender, address(this), positionIds, transferAmounts, "");

假如发现用户当前输入的 outcomeTokenAmounts 内存在负数，即存在用户将代币发送给市场的情况，我们就将 touched 设置为 true 然后调用 safeBatchTransferFrom 将资产从用户 msg.sender 转移给市场。

与上述过程相同，假如 outcomeTokenNetCost < 0，即用户需要会在市场内获得资产，此时我们会首先调用 mergePositionsThroughAllConditions 进行 merge 操作，然后遍历获得 transferAmounts:

if(outcomeTokenNetCost < 0) {
    mergePositionsThroughAllConditions(uint(-outcomeTokenNetCost));
}

emit AMMOutcomeTokenTrade(msg.sender, outcomeTokenAmounts, outcomeTokenNetCost, uint(fees));

touched = false;
for (uint i = 0; i < atomicOutcomeSlotCount; i++) {
    if(outcomeTokenAmounts[i] > 0) {
        touched = true;
        transferAmounts[i] = uint(outcomeTokenAmounts[i]);
    } else {
        transferAmounts[i] = 0;
    }
}
if(touched) pmSystem.safeBatchTransferFrom(address(this), msg.sender, positionIds, transferAmounts, "");

最后，我们需要处理 netCost < 0 情况，这种情况意味着用户可以在 Market 内获得资产，所以我们需要将该部分资产转移给用户:

if(netCost < 0) {
    require(collateralToken.transfer(msg.sender, uint(-netCost)));
}

简单来说，trade 函数会首先调用 calcNetCost 获得用户给定的 outcomeTokenAmounts 对应的 outcomeTokenNetCost 。如果 outcomeTokenNetCost > 0，那么我们会将用户的 collateral token 转移进入 Market 合约，然后执行 split 操作，将转入的 collateral token 转化为数量为 outcomeTokenNetCost 的各种类型的 condition token。反之，则会 merge outcomeTokenNetCost 数量的 condition token。在此过程中，我们也会进行各种代币转移结算。

有了上述知识后，我们就可以介绍 LSMR 算法，该算法的数学原理存在一定的复杂性，但其数学表达式较为简单，原始版本的 LSMR 的数学形式如下: $$ C(q) = b \cdot \ln(\sum_i e^{q_i / b}) $$ 此处的 $p$ 是当前市场内的所有投注选项的数量，实际上是一个列表，我们可以使用 $p_i$ 获得某一个结果的数量。 $b$ 是一个流动性参数，用于调整价格的变化速度，该参数的另一个含义是控制 LSMR 做市算法的可能损失的最大数额。这意味着 $b$ 数值越大，意味着 LSMR 提供的市场流动性越高，但这意味着一旦行情剧烈变化，做市商会亏损更多资金。在 Gnosis 实现中，b 的数值为 funding 与 $\log_2 N$ 的商，此处的 $N$ 是指当前市场内总共存在所有 Condition Token 的种类数量，即代码中的 atomicOutcomeSlotCount。而 $q_i$ 就是指当前 LSMR 算法历史上与用户交易的总和(其实就是历史交易情况的汇总，将每次交易者每次买入和卖出的数量记录下来，然后汇总就可以得到 $q_i$ 的数值)

Implementing Hanson’s Market Maker 博客内部包含大量与 LSMR 算法有关的学术文献和一些简单的阐释，该文作者曾经在雅虎工作，并为雅虎公司构造预测市场。另外，假如读者阅读了 Logarithmic Market Scoring Rules for Modular Combinatorial Information Aggregation 会发现原始版本 $s_i = a_i + b \log(r_i)$ 与上述版本不一致，这是因为上述版本并不是评分函数，而是评分函数对应的成本函数，具体推导可以参考 A Utility Framework for Bounded-Loss Market Makers

在 Gonsis 的版本内，可能是考虑到实现 ln 和 exp 算法的复杂性，所以 Gnosis 使用了 log2 和 pow2 算法替代了原始数学形式中的 ln 和 exp 函数，所以 Gnosis 版本的 LSMR 形式如下: $$ C(q) = b \cdot \log_2(\sum_i 2^{q_i / b}) $$ 我们第一步是得到 $q_i$ 的数值，我们记 $\vec{x}$ 为用户当前的交易情况，实际上就是代码内 outcomeTokenAmounts 变量，读者应该额外注意该列表内元素的正负情况含义。而 LSMR 合约的各种 condition token 余额可以使用如下方法计算： $$ \mathrm{balance} = \text{init balance} - \sum_{i-1} \vec{x_i} $$ 那么这意味着我们可以使用如下方法计算当前第 $i$ 次交易的历史累计值 $p_i$:

$$ \begin{align*} p_i &= x_{i} - \mathrm{balance}\\ &= \vec{x}_{i} + \sum_{i-1}\vec{x}_i - \text{init balance}\\ &= \sum_i \vec{x}_i - \text{init balance} \end{align*} $$

所以，我们可以看到如下用于 $p_i$ 计算的代码:

require(outcomeTokenAmounts.length == atomicOutcomeSlotCount);

int[] memory otExpNums = new int[](atomicOutcomeSlotCount);
for (uint i = 0; i < atomicOutcomeSlotCount; i++) {
    int balance = int(pmSystem.balanceOf(address(this), generateAtomicPositionId(i)));
    require(balance >= 0);
    otExpNums[i] = outcomeTokenAmounts[i].sub(balance);
}

上述公式内的 balance 代表交易前的 LSMR 持有的余额。显然 otExpNums 就是 $p_i$ 的数值。在一般的 LSMR 实现中，我们需要使用 $C(q_{new}) - C(q_{old})$ 计算出用户当前交易需要支付的资金，此处我们记用户支付的资金数量为 netCost。在 Gnosis 内，当 netCost < 0 时代表用户可以从 LSMR 智能合约内获得资金，LSMR 合约通过 merge 操作为用户提供资金；而 netCost > 0 时，代表用户需要向 LSMR 合约支付资金，合约会将用户支付的资金直接 split 为 condition token。这些机制在上文已经有所介绍。

我们在此处证明一个有趣的结论，即经过 netCost 调整后 $C(q) = 0$，即证明每一次 trade 结束后，$C(q) = b \cdot \log_2(\sum_i 2^{(q_i + \text{netCost}) / b}) = 0$。为了证明此结论，我们需要使用数学归纳法，当 $t = 1$ 即第一次用户交易。以下数学标记中，我们使用 $q^t$ 代表这是第 t 次交易时的 $q$ 值: $$ \begin{align*} C(q^1) &= b\log_2(\sum_i 2^{(q^1_i - \text{netCost}) / b})\\ &= b\log_2\bigg(2^{-\text{netCost} / b} \cdot \sum_i 2^{{q^1_i} / b}\bigg)\\ &= b\log_2\bigg(2^{-(C(q^1_i) - C(q^0_i)) / b} \cdot \sum_i 2^{{q^1_i} / b}\bigg)\\ &= b\log_2\bigg(2^{-(C(q^1_i) / b} \cdot \sum_i 2^{{q^1_i} / b}\bigg)\\ &= b\log_2\bigg(2^{-\log_2 \sum_i 2^{q^1_i / b}} \cdot \sum_i 2^{{q^1_i} / b}\bigg)\\ &= b \log_21\\ &= 0 \end{align*} $$ 我们可以发现经过 netCost 的 split 或者 merge 调整后，$C(q) = 0$ 在第一次交易(即 $t = 1$) 时是成立的。根据数学归纳法，我们假设 $t = n$ 时，上述 netCost 调整后 $C(q^n) = 0$ 仍然成立，我们需要推导 $ t = n+ 1$ 时，$C(q^{n+1}) = 0$ 也成立。

$$ \begin{align*} C(q^{n+1}) &= b\log_2(\sum_i 2^{(q^{n+1}_i - \text{netCost}) / b})\\ &= b\log_2\bigg(2^{-(C(q^{n+1}_i) - C(q^n_i)) / b} \cdot \sum_i 2^{{q^{n+1}_i} / b}\bigg)\\ &= b\log_2\bigg(2^{-(C(q^{n+1}_i) / b} \cdot \sum_i 2^{{q^1_i} / b}\bigg)\\ &= 0 \end{align*} $$

这说明任何经过 netCost 调整后，$C(q) = 0$ 是恒成立。这为我们优化代码带来了好处，因为 trade 函数会自动使用 netCost 调整，所以在计算用户需要缴纳的资金 $C(q_{new}) - C(q_{old})$ 时，由于所有的 $C(q_{old}) = 0$ 是成立的，所以用户需要支付的资金数量只等于 $C(q_{new})$。换言之，我们可以直接使用 otExpNums 带入以下公式计算，而不需要考虑通过减法计算获得用户真实需要支付的资金

$$ C(q) = b \cdot \log_2(\sum_i 2^{q_i / b}) $$ 此处我们需要考虑用户的买入和卖出对当前预测市场内所有投注结果数量的影响。然后，我们计算 log2N 的数值，该数值在计算最终的 b 时会被使用，计算代码如下:

int log2N = Fixed192x64Math.binaryLog(atomicOutcomeSlotCount * ONE, Fixed192x64Math.EstimationMode.UpperBound);

此处需要注意计算结果需要向上取整。此处的向上取整有多重安全考虑，我们会在使用 log2N 时分别介绍向上取整的安全考虑。接下来，我们需要处理一个特殊的问题，即溢出问题，在计算过程中，我们存在 $2^{q_i / b}$ 的计算，这种计算有可能导致计算结果向上溢出，所以 Gnosis 引入了 offset 变量，该变量用于控制溢出: $$ C(q) = b \cdot \bigg(\log_2(\sum_i 2^{q_i / b - \text{offset}}) + \text{offset}\bigg) $$ 此处的的 $+ \text{offset}$ 是对计算 $2^{q_i / b - \text{offset}}$ 的损失补偿，背后的数学原理是: $$ \begin{align*} \log_2\sum_i 2^{q_i / b - \text{offset}} &= \log_2\sum_i \frac{2^{q_i / b}}{2^\text{offset}}\\ &= \log_2\frac{1}{2^\text{offset}} \sum_i 2^{q_i / b}\\ &= \log_2 \sum_i 2^{q_i / b} - \text{offset} \end{align*} $$ 我们可以看到我们对 $q_1 / b$ 的 offset 调整导致计算出的 $\log_2$ 数值相比于原数值少了 offset 的数量，所以我们需要进行 + offset 补偿。那接下来的问题是如何计算出 offset 的数值，我们只需要求解如下不等式: $$ 2^{\max q_i / b - \text{offset}} \cdot \mathrm{ONE} \le 2^{256 - 8} - 1 = 2^{248} - 1 $$ 此处的 ONE 是因为 solidity 内只可以使用定点小数而增加的，在 Gnosis 实现中，所有的小数都使用了 64 位定点模式，所以此处的 ONE 数值为 $2^{64}$。对于不等式右侧，我们要求小于 $2^{256 - 8}$ 的原因是我们要使得最终的 $\sum 2^{q_i / b - \text{offset}}$ 的数值不溢出，而我们单个市场最多支持 256 种代币，所以每一个项都需要需要小于 $2^{256} / 256$ ，该数值就是 $2^{248}$。对上述不等式进行变形: $$ 2^{\max q_i / b - \text{offset}} = \frac{2^{248} - 1}{2^{64}} \approx 2^{184} $$ 继续推导可以获得 $\text{offset} = \max q_i / b - 184$ 的结论。但是需要注意的，所有的此处出现的数字都是 64bit 定点小数，所以此处的计算出的 EXP_LIMIT = 184 << 64，数值为 3394200909562557497344。这也是 sumExpOffset 函数内部的 offset 的计算原理：

require(log2N >= 0 && int(funding) >= 0);
offset = Fixed192x64Math.max(otExpNums);
offset = offset.mul(log2N) / int(funding);
offset = offset.sub(EXP_LIMIT);

其实此处的计算就要求 log2N 需要是向上取整的，因为假如此处的 log2N 是向下取整的，那么计算出的 offset 会偏小，有可能 offset 调整不足，导致最终求和计算时发生溢出。

然后 sumExpOffset 也计算出了 $\sum_i 2^{q_i / b - \text{offset}}$ 的数值，计算过程如下:

uint term;
for (uint8 i = 0; i < otExpNums.length; i++) {
    term = Fixed192x64Math.pow2((otExpNums[i].mul(log2N) / int(funding)).sub(offset), estimationMode);
    if (i == outcomeIndex)
        outcomeExpTerm = term;
    sum = sum.add(term);
}

在这里，我们会看到一个额外的 outcomeTokenIndex，在 calcNetCost 函数内部，我们并不会处理此参数，而在计算某种投注选项的价格时，我们需要处理该选项，我们会在后文中介绍。

完成上述计算后，我们最终需要计算出 netCost 的数值，此时我们只需要对刚刚计算出的 $\log_2 \text{sum}$ 进行增加 offset 与乘以 b 即可，即实现如下数学公式: $$ \text{netCost} = \frac{\text{funding}}{\text{log2N}} \times (\log_2 \text{sum} + \text{offset}) $$ 对应的代码如下:

(uint sum, int offset, ) = sumExpOffset(log2N, otExpNums, 0, Fixed192x64Math.EstimationMode.UpperBound);
netCost = Fixed192x64Math.binaryLog(sum, Fixed192x64Math.EstimationMode.UpperBound);
netCost = netCost.add(offset);
netCost = (netCost.mul(int(ONE)) / log2N).mul(int(funding));

此处的进行 binaryLog 显然需要向上取整，因为所有的舍入都应该有利于协议。我们可以看到为了保证除法的计算精度，我们在 netCost 的最终计算中使用了 (netCost.mul(int(ONE)) / log2N).mul(int(funding));，这意味着计算出的 netCost 其实是如下表达式: $$ \text{netCost} = \frac{\text{funding}}{\text{log2N}} \times (\log_2 \text{sum} + \text{offset}) \times \text{ONE} $$ 所以我们最终处理 netCost 需要除以 ONE 获得精度正确的结果:

// Integer division for negative numbers already uses ceiling,
// so only check boundary condition for positive numbers
if(netCost <= 0 || netCost / int(ONE) * int(ONE) == netCost) {
    netCost /= int(ONE);
} else {
    netCost = netCost / int(ONE) + 1;
}

在前文中，我们介绍 sumExpOffset 时提到 outcomeIndex 用于计算某种选项的价格，此处我们要给出 LSMR 算法下某种选项的边际价格的计算公式: $$ p_{\text{out}} = \frac{2^{q_{\text{out}} / b}}{\sum_i 2^{q_i / b}} $$ 上述数学公式内的所有参数都很容易利用 sumExpOffset 函数获得，所以计算边际价格的代码非常简单:

/// @dev Returns marginal price of an outcome
/// @param outcomeTokenIndex Index of outcome to determine marginal price of
/// @return Marginal price of an outcome as a fixed point number
function calcMarginalPrice(uint8 outcomeTokenIndex)
    public
    view
    returns (uint price)
{
    int[] memory negOutcomeTokenBalances = new int[](atomicOutcomeSlotCount);
    for (uint i = 0; i < atomicOutcomeSlotCount; i++) {
        int negBalance = -int(pmSystem.balanceOf(address(this), generateAtomicPositionId(i)));
        require(negBalance <= 0);
        negOutcomeTokenBalances[i] = negBalance;
    }

    int log2N = Fixed192x64Math.binaryLog(negOutcomeTokenBalances.length * ONE, Fixed192x64Math.EstimationMode.Midpoint);
    // The price function is exp(quantities[i]/b) / sum(exp(q/b) for q in quantities)
    // To avoid overflow, calculate with
    // exp(quantities[i]/b - offset) / sum(exp(q/b - offset) for q in quantities)
    (uint sum, , uint outcomeExpTerm) = sumExpOffset(log2N, negOutcomeTokenBalances, outcomeTokenIndex, Fixed192x64Math.EstimationMode.Midpoint);
    return outcomeExpTerm / (sum / ONE);
}

至此，我们就完成了关于 LSMR 算法的全部介绍。最后，我们推导一下为什么 LSMR 做市商的最大亏损是参数 $b$。在最开始，做市商的成本函数是: $$ \begin{align*} C(\vec{0}) &= b\log_2\sum_n 2^{q_i / b}\\ &=b\log_2 n \end{align*} $$ 其中 $n$ 是指当前市场内的 condition token 代币种类数量。假如最终预测市场结果确定为第一个选项，那么其他选项都会被抛售给 LSMR，而 LSMR 持有的第一个选项代币都会被卖出，此时 $$ C \begin{pmatrix} q_1 \\ -\infty \\ -\infty \\ \vdots \end{pmatrix} = b \log \left( \exp \left( {q_1 \over b} \right) \right) = q_1 $$ 交易者需要支付 $q_1 - b\log_2 n$ 的资金，同时获得 $q_1$ 的收益，总体来说，交易者获得 $b \log_2 n$ 的利润，而交易者的利润就是 LSMR 做市商损失，所以 LSMR 在此过程中亏损 $b \log_2 n$。但 Gnosis 定义: $$ b = \frac{\text{funding}}{\log_2 n} $$ 所以做市商最大亏损为 funding。

总结

本文主要介绍 Gnosis 为其预测市场开发的两个智能合约，其中 Condition token 仍被很多预测市场所使用，但是 LSMR 算法并没有被广泛使用，但是很多研究表明该算法可能是高效的。在编写本文时，我最大的收获是访问了 David Pennock 的博客。David Pennock 曾在雅虎担任研究员期间为雅虎设计预测市场，他的博客内充满了各种设计预测市场的思路和实践经验。

概述#

conditional tokens contracts#

市场初始化#

Split Position#

Merge Position#

Redeem Position#

ECMH 算法实现#

Condition tokens Market makers#

Factory 部署#

初始化#

LSMR 算法#

总结#

概述

conditional tokens contracts

市场初始化

Split Position

Merge Position

Redeem Position

ECMH 算法实现

Condition tokens Market makers

Factory 部署

初始化

LSMR 算法

总结