基于凸优化构建 AMM 路由求解算法

概述

在 AMM 领域，跨多个 AMM 进行路由优化始终是一个问题。所谓路由优化是指单笔 swap 对单个池子可能产生较大冲击，但是假如我们将该笔交易分配到多个池子，那么我们可以获得更好的交易输出。一个典型的案例是 odos 求解出的 100 ETH 兑换 USDC 的路径:

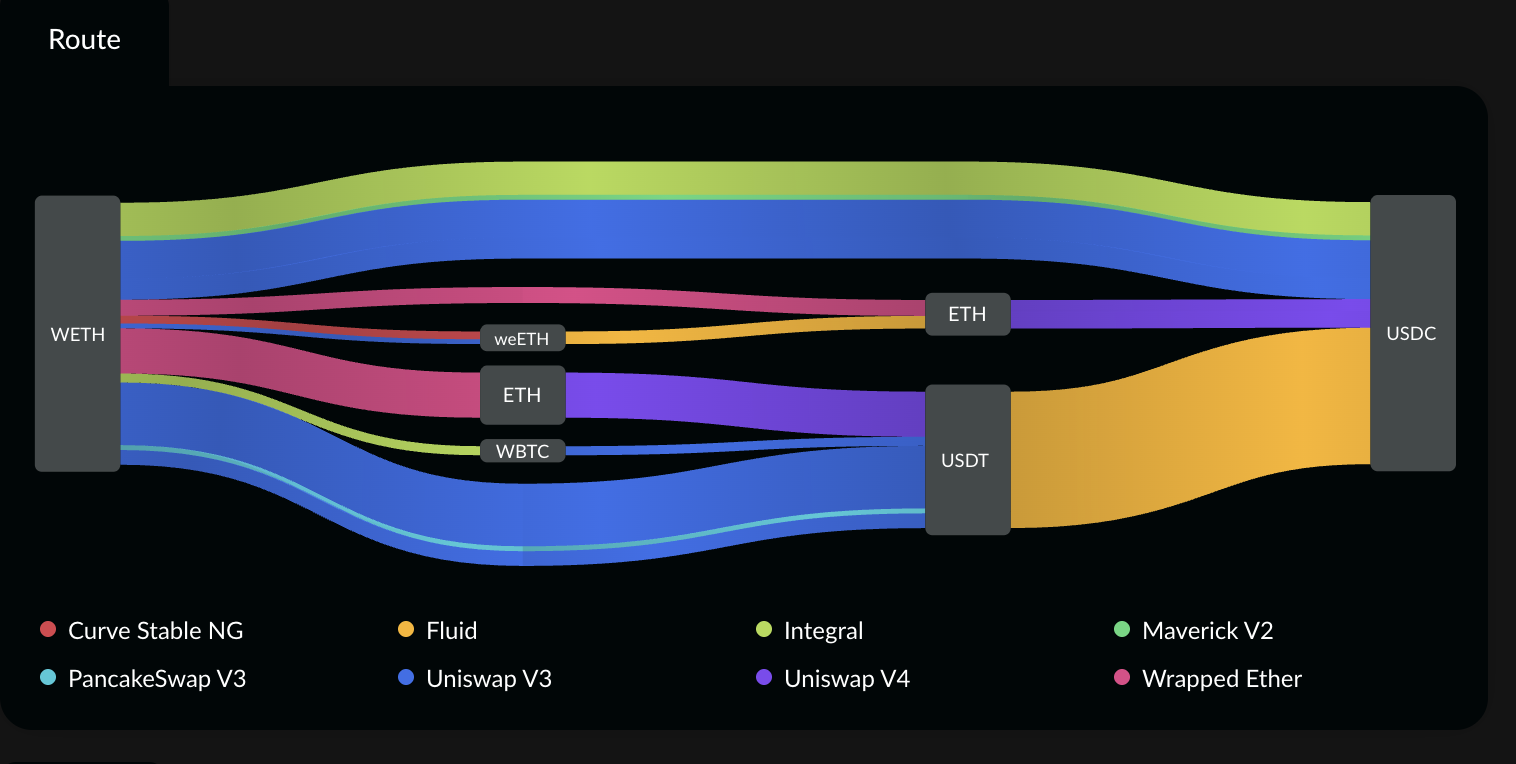
ODOS Swap

可以看到上述路径包含大量的 AMM 池子，并且每一个池子都承载了一定数量的兑换。通过上述路径，我们就可以获得最优的兑换方案。但是上述路径是如何被求解的? 该问题已有多篇论文发表，本文使用的最核心的论文是 An Eﬃcient Algorithm for Optimal Routing Through Constant Function Market Makers。当然，除了上述论文外，本文的部分内容还来自:

Optimal Routing for Constant Function Market Makers。对于部分数学符号，该论文给出了更多的解释
最优化计算方法（简化版）本文使用的凸优化的一些定理都来自该教材的第二章基础知识，读者可以简单阅读
Optimally Routing through DEXs 是核心论文作者为论文编写的 PPT，可以作为辅助材料，笔者在编写此文时并没有大量参考该材料

有幸的是，Theo Diamandis 在编写论文时，也编写了使用论文方法的 AMM 路由求解器，代码仓库为 CFMMRouter.jl，值得注意的是，该软件的文档也是编写本文的重要参考，推荐读者阅读。

为了方便读者理解后文内容，我们首先对后文描述的路由算法给出一个非正式的表述。后文给出路由算法是基于市场均衡价格运作的，原理是根据用户的需求，比如用户希望将资产 A 兑换为尽可能多的资产 B，求解器会首先根据用户的目标(即效用函数)微调市场价格，然后对所有 AMM 市场与微调后的市场价格进行套利，套利完成后继续评估效用函数，然后微调市场价格。最后，我们可以得到一个市场均衡价格，该价格使得用户的需求得到满足。

问题定义与符号说明

本节基本不涉及任何数学问题，只是对本文中使用的部分核心内容进行了符号定义和说明。

Assets.

对 $n$ 种资产进行索引，索引为 $j = 1,\dots,n$

Trading sets.

对于 markets $i = 1,\cdots,m$ ，市场内可以交易一定数量的 $n_i$。我们定义每一个市场的交易集(trading set) $T_i \subseteq R^{n_i}$。每一个交易者可以与市场交易一篮子资产 $\Delta_i \in R^{n_i}$，此处的 $\Delta_i > 0$ 代表从市场接受资产，而 $\Delta_i < 0$ 代表发送给市场资产。市场只接受满足以下条件的交易: $$ \Delta_i \in T_i $$ 我们假设 $T_i$ 是一个封闭的凸集(closed convex set) 且满足 $0 \in T_i$。

此处我们可以视 $R^{n_i}$ 是当前池子所持有的各种代币的余额情况，当然，可能的交易组合一定位于 $R^{n_i}$ 的子集内部，因为交易一定无法输出大于池子余额的情况，此处所有可能的交易组合构成了 $T_i$，不同的代币交易情况 $\Delta_i$ 也一定属于 $T_i$。理论上，我们只会给出 $\Delta_i$ 内的部分资产，比如给定几个资产的输入，要求算法给出最优的输出。

Local and global indexing

CFMM Tokens Graph

市场 $i$ 只能交易全体代币集合的子集 $n_i$，我们引入矩阵 $A_i \in R^{n \times n_i}$ 将本地索引与全局索引联系。 $A_i\Delta_i$ 代表我们在市场 $i$ 中发送或者接受的代币数量并且以全局索引记录。比如总代币集合包含 3 种代币，上述图像中 CFMM 1 可以交易所有的三种代币，所以 $A_1$ 是一个 3 ×3 identity matrix. 在 CFMM 4 中存在代币 1 和代币 3 的交易，那么我们定义: $$ A_i = \begin{bmatrix} 1 & 0 \ 0 & 0 \ 0 & 1 \end{bmatrix} $$ 假如代币 $k$ 在市场内的索引与在全局代币集合内的索引 $j$ 一致，$(A_i){jk} = 1$；否则 $(A_i){jk} = 0$。简单来说，我们可以将 $A_i$ 视为状态转移矩阵，该矩阵可以将我们使用本地索引的 $\Delta_i$ 转化为以全局索引的 $A_i\Delta_i$

Network trade vector

汇总在每一个市场内的交易情况，并将其转化为全局索引形式，我们可以得到 network trade vector: $$ \Psi = \sum_{i=1}^{n}A_i\Delta_i $$ 我们视 $\Psi$ 为在所有市场内交易的净结果。如果 $\Psi > 0$ 那么在执行所有交易 ${\Delta_i}_{i=1}^m$我们获得到一定数量资产 $i$ 。相反的，假如 $\Psi < 0$，我们会在市场内付出一定数量的资产 $i$。如果 $\Psi = 0$ 并不意味着我们没有交易资产 $i$，而是资产 $i$ 在不同交易中的支出和收入抵销。

Network trade utility

在 Network trade vector 基础上，我们定义效用函数 $U: R^n\to R \cup {-\infty}$。该效用函数作用于净交易 $\Psi$。我们假设 $U$ 是 concave 和 increasing。同时，我们需要在 $U$ 内施加约束，假如 $\Psi$ 对于交易者不可接受，那么 $U(\Psi) = -\infty$ 。我们可以为不同的任务施加不同的 $U$，比如我们可以对清算、购买代币或者寻找套利机会给出不同的 $U$。在后文中，我们将给出多个 $U$ 的形式和具体表达式。

Optimal routing problem 是指寻找有效交易，使得交易者的效用最大化: $$ \begin{array}{ll} \text{maximize} & U(\Psi) \\ \text{subject to} & \Psi = \sum_{i=1}^m A_i\Delta_i \\ & \Delta_i \in T_i, \quad i = 1, \dots, m \end{array} $$ 这是一个凸优化问题，我们可以使用凸优化方法进行求解。

CFMM 定义与数学表述

CFMM(Constant Function Market Makers) 允许任何人交易一篮子代币 $r$ 兑换成其他一篮子代币 $s$。CFMM 定义了以下三个属性:

reserves $R \in R^r_{+}$，我们记 $R_j$ 是资产 $j$ 在 CFMM 内的数量
trading function 是一个 concave function $\varphi: R^r_{+} \to R$
trading fee $0 < \gamma \le 1$

任何用户可以向 CFMM 提交 $\Delta \in R^r$。满足以下条件的交易会被 CFMM 接受: $$ \varphi(R - \gamma\Delta_--\Delta_+) \ge \varphi(R) $$ 和 $R - \gamma\Delta_--\Delta_+ \ge 0$。在上式内，$\Delta_+$ 是 $\Delta$ 内的正数部分，符合 $(\Delta_+)_j = \max\{\Delta_j, 0\}$ ，而 $\Delta_-$ 是 $\Delta$ 内的负数部分，符合 $(\Delta_-)_j = \min\{\Delta_j, 0\}$ 。$\Delta_+$ 有时被称为接受资产(received basket)，而 $\Delta_-$ 有时被称为支出资产(tendered basket)。交易集合 $T$ 在 CFMM 中定义如下: $$ T = {\Delta \in \R^r | \varphi(R - \gamma\Delta_--\Delta_+)\ge\varphi(R)} $$

在另一些文献中，比如 Optimal Routing for Constant Function Market Makers 内，我们会使用 $\Lambda$ 代表 $\Delta_+$ 并使用 $\Delta$ 代表 $\Delta_-$。实际上后文代码中也使用了 $\Lambda$ 和 $\Delta$ 符号。

$T$ 是一个 convex 而 $\varphi$ 是 concave。在用户交易后，CFMM 内的 reserves 会按照以下方式更新: $$ R \gets R - \Delta_--\Delta_+ $$ 举例说明: $$ \varphi(R) = \sqrt{R_1R_2} $$ Uniswap V3 内引入了区间流动性，区间流动性可以使用以下方程描述: $$ \varphi(R) = \sqrt{(R_1 + \alpha)(R_2 + \beta)} $$ Balancer 使用了带权重的几何平均数: $$ \varphi(R) = \prod^r_{i=1}R_i^{w_i} $$ 上述交易函数内的 $r$ 是交易资产的数量，$w \in R_+^r$ 是已知的权重且 $\mathbf{1}^Tw = 1$

Curve 使用了以下交易函数: $$ \varphi(R) = \alpha\mathbf{1}^TR-(\prod_{i=1}^rR_i^{-1}) $$

Curve 实际上是最难处理的 AMM，本文没有直接给出包含 Curve 的路由求解方法。其中一个原因是 Curve 的 AMM 不具备 homogeneous 属性。简单来说，我们可以 Cuvre 内添加流动性和撤出流动性并完全与 $R_i$ 成比例，这意味着我们可以通过增减流动性完成代币兑换。当然，Curve 的套利也没有闭式解。

求解算法

对于路由优化问题，我们会使用分解的方法，将复杂的路由问题分解为一系列简单子问题。在本节中，我们将路由问题分解并在多个市场内并行处理。

Dual decomposition

为了方便读者理解，我们首先介绍 Lagrangian Relaxation 技术。以下内容大部分直接来自 A Tutorial on Dual Decomposition and Lagrangian Relaxation for Inference in Natural Language Processing。推荐读者直接阅读该论文的前几部分。

我们假设当前存在有限集 $\mathcal{Y}$，该集合是 $\R^d$ 的子集(subset)。对于任意的向量 $y \in \mathcal{Y}$ ，存在以下评分函数: $$ h(y) = y \cdot \theta $$ 此处的 $\theta$ 也是 $\R^d$ 内的向量。我们的目标是: $$ y^\ast = \arg\max_{y \in \mathcal{Y}} h(y) = \arg\max_{y \in \mathcal{Y}} y\cdot\theta $$ 在实践中，$y$ 通常是一个 binary vector($y \in {0, 1}^d$) ，而 $\theta$ 代表每部分的评分，所以定义 $h(y) = y \cdot \theta$ 暗示着每部分的得分总和。读者不难发现上文中的: $$ \Psi = \sum_{i=1}^{n}A_i\Delta_i $$ 与此处的 $h(y)$ 形式一致并并且内涵一致。但是 $y^\ast$ 是计算困难的，在部分情况下这是一个 NP 难问题，在另一些情况下，这是一个可以在多项式时间内求解的问题，但求解算法实际运行时间很长。此处我们选择使用 Lagrangian relaxation 来优化问题。

使用 Lagrangian relaxation 的第一步是选择有限集 $\mathcal{Y}’ \subset \R^d$ 且具有以下属性:

$\mathcal{Y} \subset \mathcal{Y}'$
对于任何 $\theta \in \R^d$ ，我们容易找到 $$ \arg\max_{y \in \mathcal{Y}’} y\cdot\theta $$
最后，我们假设 $$ \mathcal{Y} = \{\, y : y \in \mathcal{Y}’ \ \text{and} \ Ay = b \,\} $$ 此处的 $A \in \R^{p \times b}$ 且 $b \in \R^b$ 。所以条件 $Ay = b$ 指在 $y$ 上存在 $p$ 个线性约束。该约束是我们上文对 $\mathcal{Y} \subset \mathcal{Y}’$ 的补偿。我们假设约束的数量 $p$ 与输入的大小存在多项式关系。

我们引入 Lagrange multipliers $u \in \R^p$ 。Lagrangian 是 $$ L(u, y) = y \cdot \theta + u \cdot (Ay - b) $$ 上述方程包含了我们最初的优化目标 $y \cdot \theta$，并且包含线性约束和 Lagrange multipliers。对偶映射(dual objective)如下: $$ L(u) = \max_{y\in\mathcal{Y}’}L(u, y) $$ 简单来说，对偶映射来自对于每一给定的 $u$ ，我们希望找到在所有的 $y \in \mathcal{Y}’$ 内最大的值，在上文，我们已经提到 $y\cdot\theta$ 是容易计算的。如此以来，我们将 $L(u, y)$ 转化为了 $L(u)$，现在我们的目标是最小化 $Ay - b$ 的惩罚。所以对偶问题是找到： $$ \min_{u \in \R^p} L(u) $$

上文中，我们介绍了 Lagrangian relaxation。回到最初的问题，我们希望求解 $U(\Psi)$ 的最大值。一般来说，我们 $U$ 都是一个线性效用函数，所以此处我们可以直接对 $U(\Psi)$ 进行 Lagrangian relaxation 处理。我们可以获得如下问题: $$ \begin{array}{ll} \text{maximize} & U(\Psi) - \nu^T(\Psi - \sum_{i=1}^mA_i\Delta_i)\\ \text{subject to} & \Delta_i \in T_i, \quad i = 1, \dots, m \end{array} $$ 上述问题中 $\Psi \in \R^n$ 。简单化简，我们可以得到: $$ \begin{array}{ll} \text{maximize} & U(\Psi) - \nu^T\Psi + \sum_{i=1}^m(A_i^T\nu)^T\Delta_i\\ \text{subject to} & \Delta_i \in T_i, \quad i = 1, \dots, m \end{array} $$ 上述方程内没有包含耦合的约束，所以我们可以分别求解 $\Psi$ 和 $\Delta_i$。接下来，我们首先对 $\Psi$ 进行求解: $$ \text{maximize}\ U(\Psi) - \nu^T\Psi $$ 此处，我们需要引入另一个凸优化中常被使用的概念——共轭函数。任何适当函数 $f$ 的共轭函数被定义为: $$ f^*(y) = \sup_{x \in \mathrm{dom}, f}{y^T x - f(x)} $$ 值得注意的是，对任意函数 $f$ 都可以定义共轭函数，其共轭函数 $f^*$ 恒为 convex function。不难发现上述 $\text{maximize}\ U(\Psi) - \nu^T\Psi$ 与 $f^*(y)$ 类似，所以我们可以改写为以下形式: $$ \bar{U}(\nu) = -U(-\nu) = \sup_\Psi(U(\Psi) - \nu^T\Psi) $$ 首先，我们不难根据 $U$ 获得 $\bar{U}$ 的闭式解。根据共轭函数的性质，上述方程一定是关于 $\nu$ 的 convex function. 另一个需要注意的细节是，假如 $\nu < 0$ ，那么 $\bar{U}(\nu) = +\infty$ ，这是因为假如 $\nu < 0$，随着 $\Psi$ 取值增加，一定会导致 $\bar{U}(\nu)$ 的值推到无穷大(注意，在本文第一节定义问题时就已经说明 $U$ 是一个增函数)

接下来，我们需要解决另一个子问题: $$ \begin{array}{ll}\text{maximize} & \sum_{i=1}^m(A_i^T\nu)^T\Delta_i\\ \text{subject to} & \Delta_i \in T_i, \quad i = 1, \dots, m\end{array} $$

我们可以将将上述最优化问题也可以被记为 $\textbf{arb}_i(A_i^T\nu)$。使用 $\textbf{arb}$ 的原因是该问题的解与无套利是一致的，换言之，当 $A_i^T\nu$ 与市场价格相同时，我们可以得到最大化的输出。同时 $\textbf{arb}_i(A_i^T\nu)$ 是 supremum over a family of aﬃne functions of $\nu$ ，由于 aﬃne functions 是凸函数，同时根据多个凸函数的 supremum 仍是凸函数，所以 $\textbf{arb}_i(A_i^T\nu)$ 是一个凸函数。

有趣的是，假如我们将该子问题视为求解套利问题，那么其实我们不需要任何凸优化方法就可以直接获得该问题的解。这是因为大部分 AMM 对套利问题都是存在闭式解的。给定一个资产 $i$ 的价格 $\nu_i$，假如该资产在 Uniswap v2 池子内的价格为 $\nu_{\text{uni}}$，且 $\nu_i \ne \nu_{\text{uni}}$。那么我们肯定可以找到一个交易，该交易将 Uniswap v2 池子内的价格推动到 $\nu_i$。注意，此处的套利是指给定一个外部价格 $\nu$ 和 AMM 的内部价格然后进行的套利，并不是三角套利等完全不需要输入的套利方式。

最后，我们讨论一下为什么 $\nu$ 可以被视为价格？为了解决此问题，我们首先引入支撑超平面定理。该定理的内容是如果 $C$ 是凸集，则在 $C$ 的任意边界点处都存在支撑超平面。而支持超平面的定义是:

给定集合 $C$ 及其边界上一点 $x_0$，如果 $a \neq 0$ 满足 $a^Tx \le a^Tx_0, \forall x \in C$，那么称集合: $$ \{x | a^Tx = a^Tx_0\} $$ 为 $C$ 在边界点 $x_0$ 处的支撑超平面。

在上文中，我们提到 $T_i$ 是一个封闭凸集，所以我们可以选择 $\Delta^*$ ,这样存在支撑超平面，该平面的 slope 是 $A_i^T\nu$，我们可以将该斜率解释为资产 $n_i$ 的边际价格(marginal prices)。原理如下，选择 $\delta \in \R^{n_i}$，且记 $\tilde{\nu} = A_i^T\nu$

根据支撑超平面的定义，存在: $$ \tilde{\nu}^T(\Delta^*+\delta) \le \tilde{\nu}^T\Delta^* $$ 化简上述不等式可以获得: $$ \tilde{\nu}\delta\le0 $$ 假如 $\delta_i$ 和 $\delta_j$ 是 $\delta$ 的内仅有的 2 个非零元素，我们可以使用向量的乘法规则获得以下结论: $$ \nu_i \delta_i + \nu_j \delta_j \le 0 $$ 进一步我们可以推导获得: $$ \delta_i \le -\frac{\tilde{v}_j}{\tilde{v}_i}\delta_j $$ 这刚好符合边际价格的定义。当然，实际上对于 Lagrangian relaxation 内的 $\nu$ 是代表价格在其他文献中亦有推导，比如在 Byod 的经典凸优化教材 Convex Optimization 内，我们可以读到以下内容:

Shadow Price

The dual problem

经过上述分解，我们在此处完整给出我们的 dual function: $$ g(\nu) = \bar{U}(\nu)+\sum_{i = 1}^m\textbf{arb}_i(A_i^T\nu) $$ 我们的对偶问题(dual problem)是: $$ \text{minimize}\ g(\nu) $$ 虽然我们定义了对偶问题，但我们没有说明对偶问题和最初需要解决的问题之间的关系。此处我们设 $\nu^*$ 是上述对偶问题的最优解。设 dual function 是可微的，我们可以得到如下导数: $$ \nabla g(\nu^*) = 0 $$ 使用 chain rule，我们可以得到上述 $\nabla g(\nu)$ 的具体解析式: $$ \nabla g(\nu) =\bar{U}(\nu)’ + \sum_{i = 1}^mA_i\Delta_i $$ 使用 Julia 代码描述，此处的目标函数 $g(\nu)$ 如下:

# Objective function
function fn(v)
    if !all(v .== r.v)
        find_arb!(r, v)
        r.v .= v
    end

    acc = 0.0

    for (Δ, Λ, c) in zip(r.Δs, r.Λs, r.cfmms)
        acc += @views dot(Λ, v[c.Ai]) - dot(Δ, v[c.Ai])
    end

    return f(r.objective, v) + acc
end

在代码实现中，我们使用 $\Lambda$ 代表 $\Delta_+$ 并使用 $\Delta$ 代表 $\Delta_-$，所以上述方程内的 $\Delta_i$ 在此处被表述为 $\Lambda A_i - \Delta A_i$，即代码中的 acc += @views dot(Λ, v[c.Ai]) - dot(Δ, v[c.Ai])。而上述代码内的 f 就是上文中介绍的 $\bar{U}(\nu)$。注意，此处的 find_arb! 就是上文内提到的 $\textbf{arb}_i$ 函数，其实现如下:

function find_arb!(r::Router, v)
    Threads.@threads for i in 1:length(r.Δs)
        find_arb!(r.Δs[i], r.Λs[i], r.cfmms[i], v[r.cfmms[i].Ai])
    end
end

具体来说，该函数会调用每一个市场内的 find_arb! 函数寻找每一个市场内的套利机会，由于不同市场并不互相影响，所以这是一个 Embarrassingly Parallel 问题，可以直接并行。

由于我们使用梯度求解优化问题，求解器需要我们提供 $\nabla g(\nu)$ 的值，所以代码内也实现了如下函数:

# Derivative of objective function
function g!(G, v)
    G .= 0

    if !all(v .== r.v)
        find_arb!(r, v)
        r.v .= v
    end
    grad!(G, r.objective, v)

    for (Δ, Λ, c) in zip(r.Δs, r.Λs, r.cfmms)
        @views G[c.Ai] .+= Λ .- Δ
    end

end

其中 grad! 是用户在实现 $\bar{U}(\nu)$ 时必须要实现的该效用函数的导数。

求解 dual problem

问题求解可以直接使用求解器解决。在 Julia 代码内，要求用户输入:

object 目标函数，即上文内提到的 $\bar{U}$
find_arb! 用于计算套利行为，即上文内提到的 $\textbf{arb}_i(A_i^T\nu)$

在此处，我们介绍几个在 CFMMRouter 的源代码内出现的 object function。第一个是较为简单的 LinearNonnegative ，该函数的数学形式如下，该函数用于套利。注意，此处的套利与上文中的 $\textbf{arb}_i(A_i^T\nu)$ 并不一致，此处的套利指的是在输入的多个市场 $i$ 中进行最大化套利，而上文中的 $\textbf{arb}_i(A_i^T\nu)$ 只适用于单个市场。

对于套利问题，我们可以得到以下效用函数: $$ U(\Psi) = c^T\Psi - \mathbf{I}(\Psi \geq 0) $$ 其中 $c^T$ 是由正数构建的价格向量，而 $\mathbf{I}(\Psi \geq 0)$ 是 indicator function，当 $\Psi \geq 0$ 时，$\mathbf{I}(\Psi \geq 0) = 0$，而当 $\Psi < 0$ 时， $\mathbf{I}(\Psi \geq 0) = +\infty$。$+\infty$ 对于求解器的含义是当前取值不合理，即我们通过 $\mathbf{I}(\Psi \geq 0)$ 约束求解器不要产生包含负数的 $\Psi$。换言之，我们需要构建一个只包含正数的 $\Psi$，因为这代表我们没有支付任何代币但获得了代币。

但是我们需要 $\bar{U}(\nu)$ 而不是 $U(\Psi)$，根据上文的推导，我们可以使用以下函数将 $U(\Psi)$ 转化为 $\bar{U}(\Psi)$ $$ \bar{U}(\nu) = -U(-\nu) = \sup_\Psi(U(\Psi) - \nu^T\Psi) $$ 我们可以进行如下推导: $$ \begin{align} \bar{U}(\nu) &= \sup_\Psi(U(\Psi) - \nu^T\Psi) \\ &= \sup_\Psi((c - \nu)^T\Psi - \mathbf{I}(\Psi \geq 0)) \end{align} $$ 对其进行分类讨论，当 $c > \nu$ 时，此时上确界 $\bar{U}(\nu) = +\infty$。而当 $c \leq \nu$ 时，此时上确界 $\bar{U}(\nu) = 0$。所以我们可以得到以下代码:

struct LinearNonnegative{T} <: Objective
    c::AbstractVector{T}
    function LinearNonnegative(c::Vector{T}) where {T<:AbstractFloat}
        all(c .> 0) || throw(ArgumentError("all elements must be strictly positive"))
        return new{T}(
            c,
        )
    end
end
LinearNonnegative(c::Vector{T}) where {T<:Real} = LinearNonnegative(Float64.(c))

function f(obj::LinearNonnegative{T}, v) where {T}
    if all(obj.c .<= v)
        return zero(T)
    end
    return convert(T, Inf)
end

function grad!(g, obj::LinearNonnegative{T}, v) where {T}
    if all(obj.c .<= v)
        g .= zero(T)
    else
        g .= convert(T, Inf)
    end
    return nothing
end

另一个常用的目标函数是 BasketLiquidation。该目标函数是将一篮子输入代币转化为同一个代币，所以该目标函数接受两个参数，第一个参数是 i，用以说明目标资产的索引，另一个参数是 Δin 用于给定输入资产的数组。构建代码如下:

struct BasketLiquidation{T} <: Objective
    i::Int
    Δin::Vector{T}
    
    function BasketLiquidation(i::Integer, Δin::Vector{T}) where {T<:AbstractFloat}
        !(i > 0 && i <= length(Δin)) && throw(ArgumentError("Invalid index i"))
        return new{T}(
            i,
            Δin,
        )
    end
end

该目标函数的数学表达如下: $$ \Psi_i - \mathbf{I}(\Psi_{-i} + Δ^\mathrm{in}_{-i} = 0, ~ \Psi_i \geq 0) $$ 此处的 $\Psi_{-i} $ 代表去掉索引 $i$ 的 $\Psi$ 向量，相似的，$Δ^\mathrm{in}_{-i}$ 代表去掉索引 $i$ 的代币输入。上述 $\mathbf{I}(\Psi_{-i} + Δ^\mathrm{in}_{-i} = 0, ~ \Psi_i \geq 0)$ 也属于 indicator function，对于不满足条件的情况(即 $\Psi_{-i} + Δ^\mathrm{in}_{-i} \ne 0$) 的情况，$\mathbf{I}(\Psi_{-i} + Δ^\mathrm{in}_{-i} = 0, ~ \Psi_i \geq 0) = +\infty$，以此告知求解器当前输入不符合条件。而对于满足条件的情况(即 $\Psi_{-i} + Δ^\mathrm{in}_{-i} = 0$，该等式成立意味着输入 $Δ^\mathrm{in}$ 内除了预期输出外的所有代币都已经被消耗)，$\mathbf{I}(\Psi_{-i} + Δ^\mathrm{in}_{-i} = 0, ~ \Psi_i \geq 0) = 0$

当然，上述目标函数也是 $U(\Psi)$ 的表达式，我们需要将其转化为 $\bar{U}(\nu)$ 的表达式: $$ \begin{align} \bar{U}(\nu) &= \sup_\Psi(U(\Psi) - \nu^T\Psi) \\ &= \sup_\Psi((1 - \nu^T)\Psi_i - \mathbf{I}(\Psi_{-i} + Δ^\mathrm{in}_{-i} = 0, ~ \Psi_i \geq 0) ) \end{align} $$ 我们首先分析 $(1 - \nu) > 0$ 的情况，此时 $\bar{U}(\nu) = +\infty$。接下来，我们考虑 $(1 - \nu) \le 0$ 的情况，此时 $\max \Psi_{-i} = -\Delta^\mathrm{in}_{-i}$，所以 $\bar{U}(\nu) = (\nu - 1)\Delta^\mathrm{in}_{-i}$。当然，在代码中，我们使用了 $\sum\nu\Delta^\mathrm{in}_{-i}$ 的形式:

function f(obj::BasketLiquidation{T}, v) where {T}
    if v[obj.i] >= 1.0
        return sum(i->(i == obj.i ? 0.0 : obj.Δin[i]*v[i]), 1:length(v))
    end
    return convert(T, Inf)
end

此处的 sum 计算的就是 Δin 内除了目标输出外剩下的元素与 $\nu$ 的乘积之和。本质上与上文给出的 $(\nu - 1)\Delta^\mathrm{in}_{-i}$ 是基本一致的的。而梯度计算的方法如下:

function grad!(g, obj::BasketLiquidation{T}, v) where {T}
    if v[obj.i] >= 1.0
        g .= obj.Δin
        g[obj.i] = zero(T)
    else
        g .= convert(T, Inf)
    end
    return nothing
end

简单来说，其实就是上文中的 $\bar{U}(\nu) = (\nu - 1)\Delta^\mathrm{in}_{-i}$ 的导数 $\bar{U}(\nu)’ = \Delta^\mathrm{in}_{-i}$。在此处，我们可以简单介绍 lower_limit 和 upper_limit 的计算。lower_limit 和 upper_limit 代表目标函数中 $\nu$ 的最大值和最小值，会被用于求解器求解。我们不难看出 $\min \sum\nu\Delta^\mathrm{in}_{-i} = \min\sum\epsilon$ (此处的 $\epsilon$ 代表浮点数系统内数字 $1$ 到下一个可表示数字之间的间隔)，所以 $\min\nu = \sqrt{\epsilon}$，特殊情况是 $\nu_i = 1 + \sqrt{\epsilon}$。

@inline function lower_limit(o::BasketLiquidation{T}) where {T}
    ret = Vector{T}(undef, length(o.Δin))
    fill!(ret, sqrt(eps()))
    ret[o.i] = one(T) + sqrt(eps())
    return ret
end

最后，我们介绍 BasketLiquidation 的衍生版本 Swap。该目标函数实现的是大部分用户最常见的需求，将某一种代币转化为另一种代币。该效用函数本质上是只有单种代币输入的 BasketLiquidation，代码如下:

function Swap(i::Int, j::Int, δ::T, n::Int) where {T<:AbstractFloat}
    Δin = zeros(T, n)
    Δin[j] = δ
    return BasketLiquidation(i, Δin)
end

使用数学描述效用函数如下： $$ \Psi_i - \mathbf{I}(\Psi_{[n]\setminus{i,j}} = 0,; {\Psi_j = -\delta}) $$ 由于我们已经在上文分析过了 BasketLiquidation 的特性，而 Swap 本质上就是 BasketLiquidation，所以此处不再赘述。

套利闭式解

通用市场

在上一节分析代码时，我们可以看到 find_arb! 函数是我们需要实现的，只要把 fin_arb! 函数实现，我们就可以真正实现路由求解。但是不同的市场是存在不同的套利闭式解的，本节我们会推导几个市场的套利闭式解。

在 AMM 内，输入代币和输出代币存在一一对应的关系，在一定流动性下，输入 $\delta$ 单位的代币 1 最多获得 $\lambda$ 单位的代币 2。在只考虑两种代币的情况下，交易集 $T \sube \R^2$，存在如下情况: $$ f_1(\delta_1) = \sup\{\lambda_2 | (-\delta_1,\lambda_2) \in T\}, f_2(\delta_2) = \sup\{\lambda_1 | (\lambda_1,-\delta_2) \in T\} $$ 上述表达式中 $f_1(\delta_1)$ 指向 AMM 输入 $\delta$ 单位的代币 1 ，用户最多可以获得 $\lambda_2$ 单位的代币 2，注意此处的 $T$ 是对用户而言的，所以此处使用的是 $(-\delta_1, \lambda_2)$。而 $f_2(\delta_2)$ 则是相反的使用 $\delta_2$ 单位的代币 2 最多从 AMM 处获得 $\lambda_1$ 单位代币 1。

在有了上述定义后，我们也定义如下交易函数: $$ \varphi(R_1 + \gamma\delta_1, R_2 - f_1(\delta_1)) = \varphi(R_1,R_2) $$ 此处的 $\gamma$ 代表交易手续费。我们在上文展示过该交易函数的不等式版本 $\varphi(R - \gamma\Delta_--\Delta_+) \ge \varphi(R)$。不难写出对于 $f_2(\delta_2)$ 也有类似的交易函数。

因为交易集 $T$ 是 convex，所以 $f_1$ 和 $f_2$ 都是 concave 且非负数的。在 $f_1$ 和 $f_2$ 一致的情况下，使用 $f_j$ 表示交易函数。我们定义 $f_j$ 的导数 $f_j’$ 是接受资产(received asset) 以发送资产(tendered asset) 为单位的边际报价，定义如下: $$ f_j’(\delta_j) = \lim_{h\to0^+}\frac{f_j(\delta_j + h) - f_j(\delta_j)}{h} $$ 我们的核心是讨论套利问题，在上文中，我们已经给出了套利问题的表述: $$ \begin{array}{ll} \text{maximize} & \sum_{i=1}^m(A_i^T\nu)^T\Delta_i\\ \text{subject to} & \Delta_i \in T_i, \quad i = 1, \dots, m\end{array} $$ 此处，我们使用上文中的符号重写该问题，我们简化使用 $(\nu_1, \nu_2) \ge 0$ 替代上文中的 $A_i^T\nu$。对于 $f_1$，我们可以获得以下问题表述: $$ \begin{array}{ll} \text{maximize} & -\nu_1\delta_1+\nu_2f_1(\delta_1)\\ \text{subject to} & \delta_1 \ge 0, \end{array} $$ 相似的，对于函数 $f_2$，我们可以得到以下套利问题表述: $$ \begin{array}{ll}\text{maximize} & \nu_1f_2(\delta_2) - \nu_2\delta_2\\ \text{subject to} & \delta_2 \ge 0, \end{array} $$ 肯定有读者好奇，上述公式在单一市场内肯定无法优化，因为单一市场一定没有套利机会。这里需要注意的 $\nu_1$ 和 $\nu_2$ 实际上来自路由求解问题，我们可以认为 $\nu$ 代表目前市场内的均衡价格，而对于单个市场而言，可能出现价格与市场均衡价格不符的情况，其实算是套利问题描述就是指如何在这种价格不符情况下计算出需要多少代币交易可以将价格推回 $\nu$。

理论上讲，我们需要分别求解上述两个套利问题，但众所周知，大部分 AMM 都是具有路径不依赖性，实际上两个套利问题中只会有一个存在正解，所以我们可以通过计算正负数值快速判断我们需要求解哪一个问题。而对于问题的求解方法，最简单的方法是直接二分查找，理论上可以快速找到最优解 $\delta_1^*$ 或 $\delta_2^*$。具体求解哪一个可以视问题情况确定。无论如何一定会有 $\delta_1^* \ge 0$ 或 $\delta_2^* \ge 0$ 两者中的一个不等式成立。假如出现 $\delta_1^* < 0, \delta_2^* < 0$ 的情况，此时我们一定会进行交易；而出现 $\delta_1^* > 0, \delta_2^* > 0$ 的情况则意味着 AMM 出现了漏洞，为用户发送了免费资产。

我们尝试对以下问题进行求解: $$ \begin{array}{ll}\text{maximize} & -\nu_1\delta_1+\nu_2f_1(\delta_1)\ \text{subject to} & \delta_1 \ge 0, \end{array} $$ 首先考虑 $f_1’(0) \le \frac{\nu_1}{\nu_2}$ 的情况，此处的 $f_1’(0)$ 的经济含义是当前 AMM 的边际价格，此时我们不能使用通过卖出资产 1 套利，此时上述问题的最优解是 $\delta_1^* = 0$.换言之，在这种情况下，我们放弃使用 $\delta_1$ 套利而是使用 $\delta_2$ 套利是可行的。

当然，对于 $f’_1(1) > \frac{\nu_1}{\nu_2}$ 的情况，此时我们可以进行套利，且最优解是: $$ \delta_1^* = \sup\{\delta\ge0 | f’(\delta) \ge \frac{\nu_1}{\nu_2}\} $$ 上述解的经济含义是支付一定数量的 $\delta_1^*$ 将当前 AMM 的价格推动到 $\frac{\nu_1}{\nu_2}$ (该价格代表市场价格)。

通过上述讨论，我们其实可以获得不可交易集合，即在该区间内，$\delta_1^* = 0, \delta_2^* = 0$，该不可交易区间如下: $$ f’_1(0) \le \frac{\nu_1}{\nu_2} \le \frac{1}{f’_2(0)} $$ 此时价格既不过高也不过低，无法进行任何套利交易。上述不可交易区间产生的部分原因是因为 AMM 内存在手续费 $\gamma$ 产生的。那么我们似乎还是没有回答上述问题，即如何计算套利需要多少代币呢？其实我们只需要根据套利方向，比如使用 $f_1$ 还是 $f_2$ 求解一下数学方程: $$ f’_1(\delta_1) = \frac{\nu_1}{\nu_2} $$ 或者: $$ f_2’(\delta_2) = \frac{\nu_2}{\nu_1} $$ 对于大部分 AMM 而言，$f’_1$ 或 $f’_2$ 都是具有闭式解的，很容易推导出 $\delta_1$ 或 $\delta_2$ 的表达式。

几何平均数市场

所谓几何平均数市场，指的是存在以下不变量的市场: $$ \varphi(R) = R_1^wR_2^{1-w} $$ 实际上，Uniswap V2 是 $w = \frac{1}{2}$ 的特例。使用 $\varphi(R_1 + \gamma\delta_1, R_2 - f_1(\delta_1)) = \varphi(R_1,R_2)$ 。我们可以推导: $$ \begin{align} (R_1 + \gamma\delta_1)^w(R_2 - f_1(\delta_1))^{1 - w} &= R_1^w R_2^{1 -w}\\ (R_2 - f_1(\delta_1))^{1 - w}&=\frac{R_1^w R_2^{1 -w}}{(R_1 + \gamma\delta_1)^w}\\ (R_2 - f_1(\delta_1))^{1 - w}&=\frac{ R_2^{1 -w}}{(1 + \gamma\delta_1 / R_1)^w}\\ (R_2 - f_1(\delta_1))^{1 - w}&=(\frac{ R_2}{(1 + \gamma\delta_1 / R_1)^\eta})^{1 -w}\\ R_2 - f_1(\delta_1)&=\frac{ R_2}{(1 + \gamma\delta_1 / R_1)^\eta}\\ f_1(\delta_1) &= R_2(1 - (\frac{1}{1 + \gamma\delta_1 / R_1})^\eta) \end{align} $$ 上述公式内的 $\eta = w / (1 - w)$ 。所以对于 Uniswap v2 而言，$\eta = 1$。下一步，我们求出 $f’_1(\delta_1)$ 的表达式: $$ \begin{align} f_1’(\delta_1) &= \frac{\gamma}{R_1}(-\frac{1}{(1 + \gamma\delta_1 / R_1)^2})(\eta (\frac{1}{1 + \gamma\delta_1 / R_1})^{\eta -1})(-1)R_2\\ f_1’(\delta_1) &= \eta\gamma\frac{R_2}{R_1}\frac{1}{(1 + \gamma\delta_1 / R_1)^{\eta +1}} \end{align} $$ 接下来，我们需要求解 $f’_1(\delta_1) = \nu_1 / \nu_2$ 的解析解: $$ \begin{align} \frac{R_2}{R_1}\eta\gamma\frac{1}{(1 + \gamma\delta_1 / R_1)^{\eta +1}} &= \frac{\nu_1}{\nu_2}\\ (1 + \gamma\delta_1 / R_1)^{\eta +1} &= \eta\gamma\frac{R_2}{R_1}\frac{\nu_2}{\nu_1}\\ \gamma\delta_1 / R_1 &= (\eta\gamma\frac{R_2}{R_1}\frac{\nu_2}{\nu_1})^{1 / (\eta + 1)} - 1\\ \delta_1 &= \frac{R_1}{\gamma}\Bigg((\eta\gamma\frac{R_2}{R_1}\frac{\nu_2}{\nu_1})^{1 / (\eta + 1)} - 1\Bigg) \end{align} $$ 我们可以通过上述 $\delta_1$ 计算给定价格需要支付多少代币 1 进行套利。对于 $\delta_2$ 的情况，读者可以自行求解。我们首先看一个简单情况，对于 Uniswap v2 而言，上述 $\delta_1$ 的计算会被简化为: $$ \begin{align} \delta_1 &= \frac{R_1}{\gamma}\Bigg(\sqrt{\gamma\frac{R_2}{R_1}\frac{\nu_2}{\nu_1}} - 1\Bigg)\\ &=\sqrt{\gamma\frac{R_2}{R_1}\frac{\nu_2}{\nu_1} * \frac{R_1^2}{\gamma^2}} - \frac{R_1}{\gamma}\\ &= \sqrt{R_1R_2\frac{\nu_2}{\nu_1}\frac{1}{\gamma}} - \frac{R_1}{\gamma}\\ &= \frac{1}{\gamma}(\sqrt{R_1R_2\frac{\nu_2}{\nu_1}{\gamma}} - R_1) \end{align} $$ 所以我们可以得到以下代码:

# See App. A of "An Analysis of Uniswap Markets"
@inline prod_arb_δ(m, r, k, γ) = max(sqrt(γ*m*k) - r, 0)/γ
@inline prod_arb_λ(m, r, k, γ) = max(r - sqrt(k/(m*γ)), 0)

# Solves the maximum arbitrage problem for the two-coin constant product case.
# Assumes that v > 0 and γ > 0.
function find_arb!(Δ::VT, Λ::VT, cfmm::ProductTwoCoin{T}, v::VT) where {T, VT<:AbstractVector{T}}
    R, γ = cfmm.R, cfmm.γ
    k = R[1]*R[2]

    Δ[1] = prod_arb_δ(v[2]/v[1], R[1], k, γ)
    Δ[2] = prod_arb_δ(v[1]/v[2], R[2], k, γ)

    Λ[1] = prod_arb_λ(v[1]/v[2], R[1], k, γ)
    Λ[2] = prod_arb_λ(v[2]/v[1], R[2], k, γ)
    return nothing
end

由于 Uniswap v2 套利计算很简单，所以开发者在此处并没有进行任何条件判断，而是将所有情况都计算了，这里的 prod_arb_δ 和 prod_arb_λ 内的 max 函数就是用于假如套利条件不允许，那么调用 sqrt(γ*m*k) - r 计算出是负数，通过 max 避免负数影响。

完整版本的通用几何平均数的套利求解也很简单，只是多了 $\eta$ 参数:

@inline geom_arb_δ(m, r1, r2, η, γ) = max((γ*m*η*r1*r2^η)^(1/(η+1)) - r2, 0)/γ
@inline geom_arb_λ(m, r1, r2, η, γ) = max(r1 - ((r2*r1^(1/η))/(η*γ*m))^(η/(1+η)), 0)

# Solves the maximum arbitrage problem for the two-coin geometric mean case.
# Assumes that v > 0 and w > 0.
function find_arb!(Δ::VT, Λ::VT, cfmm::GeometricMeanTwoCoin{T}, v::VT) where {T, VT<:AbstractVector{T}}
    R, γ, w = cfmm.R, cfmm.γ, cfmm.w

    η = w[1]/w[2]

    Δ[1] = geom_arb_δ(v[2]/v[1], R[2], R[1], η, γ)
    Δ[2] = geom_arb_δ(v[1]/v[2], R[1], R[2], 1/η, γ)

    Λ[1] = geom_arb_λ(v[1]/v[2], R[1], R[2], 1/η, γ)
    Λ[2] = geom_arb_λ(v[2]/v[1], R[2], R[1], η, γ)
    return nothing
end

区间流动性市场

在 Uniswap v3 等区间流动性 AMM 内，我们该如何进行套利交易。在这些系统内，我们的目标是进行 最大可行交易。所谓最大可行交易指的是找到一个合理区间，在该区间内，我们的套利可以获得收益同时交易数量最大，使用数学语言描述为 $f_1(\delta) = \sup f_1$. $$ \delta_1^- = \inf{\delta_1 \ge 0 | f_1(\delta_1) = \sup f_1} $$

实际上寻找合理区间的方法并没有严格的数学方法，目前最通用的方法就是简单的使用 for 循环迭代多个 tick 进行聚合分组，我们可以使用 liquidityNet 进行聚合。假如读者对 Uniswap v3 区间流动性感兴趣，欢迎阅读我的博客现代 DeFi: Uniswap V3

上述表达式内的 $\inf$ 代表取下界而 $\sup$ 代表取上界。$\delta_1^-$ 是指给定数量的资产 1 交易市场可以给出最大数量资产 2。基于上述定义，我们定义 minimum supported price ，该定义指 $f_1$ 在 $\delta_1^-$ 的左导数(left derivative): $$ f_1^-(\delta_1^-) = \lim_{h \to 0^+}\frac{f(\delta_1^- - f(\delta^-_1-h))}{h} $$ 此处也存在不可交易区间: $$ f_1^-(\delta_1^-) < \frac{\nu_1}{\nu_2} < \frac{1}{f_2^-(\delta_2^-)} $$ 上述讨论稍有抽象，我们在此处给出 Bounded liquidity 的案例。首先 Bounded liquidity 的 AMM 不变量表达式如下: $$ \varphi(R) = \sqrt{(R_1 + \alpha)(R_2 + \beta)}. $$ 实际上，我们可以将 Uniswap v3 的流动性区间视为上述的 AMM 表达式。基于上述 AMM 表达式和前文给出的 AMM 不变量条件 $\varphi(R_1 + \gamma \delta_1, R_2 - f_1(\delta_1)) = \varphi(R_1, R_2)$ ，我们可以给出 $f_1(\delta)$ 的定义: $$ f_1(\delta) = \min{R_2, \frac{\gamma\delta(R_2 + \beta)}{R_1 + \gamma\delta+\alpha}} $$

推导过程如下:

$$ \begin{align} \varphi(R_1 + \gamma \delta_1, R_2 - f_1(\delta_1)) &= \varphi(R_1, R_2) \\ \sqrt{(R_1 + \alpha + \gamma \delta_1)(R_2 + \beta - f_1(\delta_1))} &= \sqrt{(R_1 + \alpha)(R_2 + \beta)} \\ (R_1 + \alpha + \gamma \delta_1)(R_2 + \beta - f_1(\delta_1)) &= (R_1 + \alpha)(R_2 + \beta) \\ R_2 + \beta - f_1(\delta_1) &= \frac{(R_1 + \alpha)(R_2 + \beta)}{R_1 + \alpha + \gamma \delta_1} \end{align} $$

此处使用 $\min$ 的原因是在 Bounded liquidity 下，AMM 输出的代币最大数量只能是 $R_2$。在上文中，我们给出的 $\delta_1^-$ 的定义是给定数量的资产 1 可以换取的最大资产 2 的数量，显然，当我们耗尽 AMM 内的资产时，就可以 swap 获得最大数量的资产 2，由此可以获得等式 $f_1(\delta^-_1) = R_2$，可以解出如下结论 $$ \delta_1^- = \frac{1}{\gamma}\frac{R_2}{\beta}(R_1 + \alpha) $$ 推导过程如下: $$ \begin{align} R_2 &= \frac{\gamma\delta(R_2 + \beta)}{R_1 + \gamma\delta+\alpha} \\ R_2(R_1 + \gamma\delta+\alpha) &= \gamma\delta(R_2 + \beta)\\ \frac{1}{\gamma}R_1R_2 + \delta R_2 + \frac{\alpha}{\gamma} R_2 &= \delta(R_2 + \beta) \\ \frac{1}{\gamma} R_2 (R_1 + \alpha) &= \delta\beta \\ \delta &= \frac{1}{\gamma} \frac{R_2}{\beta} (R_1 + \alpha) \end{align} $$ 将其带入可以获得: $$ f^-_1(\delta_1^-) = \gamma\frac{\beta^2}{(R_1 + \alpha)(R_2 + \beta)} $$ 推导过程如下，第一步化简使用了复合函数的求导法则(上导下不导减去下导上不导): $$ \begin{align} f_1^-(\delta_1^-) &= \frac{\gamma(R_2 + \beta)(R_1 + \gamma\delta+\alpha) - \gamma^2\delta(R_2 + \beta)}{(R_1 + \gamma\delta+\alpha)^2}\\ &= \frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{(R_1 + \gamma\delta+\alpha)^2}\\ &= \frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{(R_1 + \frac{R_2}{\beta}(R_1+ \alpha) + \alpha)^2}\\ &= \beta^2\frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{(R_1\beta + {R_2}(R_1+ \alpha) + \alpha\beta)^2} \\ &= \beta^2\frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{((R_1 + \alpha)(R_2+\beta))^2}\\ &= \gamma\frac{\beta^2}{(R_1 + \alpha)(R_2 + \beta)} \end{align} $$ 读者可以自行对 $f_2$ 进行相关计算。上述推导过程中公式: $$ \begin{align} f_1^-(\delta) = \frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{(R_1 + \gamma\delta+\alpha)^2} &= \text{Price}\\ \gamma(R_2 + \beta)(R_1 + \alpha) &= \text{Price} * (R_1 + \gamma\delta+\alpha)^2\\ \frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{\text{Price}} &= (R_1 + \gamma\delta+\alpha)^2\\ \sqrt{\frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{\text{Price}}} &= R_1 + \gamma\delta+\alpha\\ \gamma\delta &= \sqrt{\frac{\gamma(R_2 + \beta)(R_1 + \alpha)}{\text{Price}}}-(R_1 + \alpha) \end{align} $$ 此处我们在方程右侧保留 $\gamma\delta$ 的原因是这样右侧显示较为简单。我们会在所有计算的最后将 $\gamma$ 除去。上述计算对应如下代码:

# Considers fee-free arb in the (easy) case that the price is above the current price.
# (This is enough since we can just swap the reserves and constants and re-solve the problem.)
function find_arb_pos(t::BoundedProduct{T}, price) where T
    # See Appendix A, geometric mean trading function
    δ = sqrt(t.k/price) - (t.R_1 + t.α)

    if δ <= 0
        return 0.0, 0.0
    end

    δ_max = t.k/t.β - (t.R_1 + t.α)
    if δ >= δ_max
        return δ_max, t.R_2
    end
    
    λ = (t.R_2 + t.β) - sqrt(price*t.k)

    return δ, λ
end

值得注意的，此处传入的 price 是 p/γ。所以在上述函数内并没有出现 γ 的身影。

最终，我们记 $k = (R_1 + \alpha)(R_2 + \beta)$，最终可以获得以下对于区间流动性市场的不可交易区间 $$ \frac{\gamma\beta^2}{k} < \frac{\nu_1}{\nu_2} < \frac{k}{\gamma\alpha^2} $$

在代码内，我们描述如下:

# No-arb interval (eq (17) in paper)
if γ*cfmm.current_price <= p <= cfmm.current_price/γ
    return nothing
end

概述#

问题定义与符号说明#

CFMM 定义与数学表述#

求解算法#

Dual decomposition#

The dual problem#

求解 dual problem#

套利闭式解#

通用市场#

几何平均数市场#

区间流动性市场#

概述